Распределение Парето

Распределение Парето

Плотность вероятности $x_m = 1$
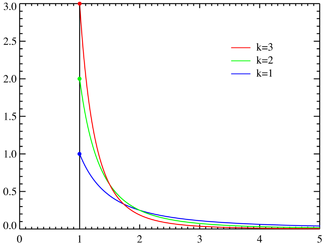
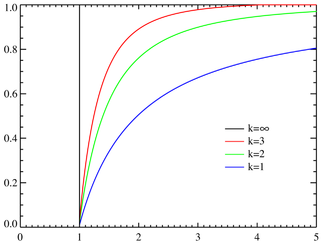
Функция распределения $x_m = 1$
Обозначение	{{{notation}}}
Параметры	$x_{m}>0\,$ - коэффициент масштаба $k>0\,$
Носитель	$x \in [x_\mathrm{m}; +\infty)\!$
Плотность вероятности	$\frac{k\,x_\mathrm{m}^k}{x^{k+1}}\!$
Функция распределения	$1-\left(\frac{x_\mathrm{m}}{x}\right)^k\!$
Математическое ожидание	$\frac{\,kx_\mathrm{m}}{k-1}\!$, если $k>1\!$
Медиана	$x_\mathrm{m} \sqrt[k]{2}$
Мода	$x_\mathrm{m}\,$
Дисперсия	$\left(\frac{x_\mathrm{m}}{k-1}\right)^2\frac{k}{k-2}\!$ при $k>2\!$
Коэффициент асимметрии	$\frac{2(1+k)}{k-3}\,\sqrt{\frac{k-2}{k}}\!$ при $k>3\!$
Коэффициент эксцесса	$\frac{6(k^3+k^2-6k-2)}{k(k-3)(k-4)}\!$ при $k>4\!$
Информационная энтропия	$\ln\left(\frac{k}{x_\mathrm{m}}\right) - \frac{1}{k} - 1\!$
Производящая функция моментов	не определена
Характеристическая функция	$k(-ix_\mathrm{m}t)^k\Gamma(-k,-ix_\mathrm{m}t)\,$

Распределе́ние Паре́то в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений, являющихся степенными. Называется по имени Вилфредо Парето. Встречается при исследовании различных явлений, в частности, социальных, экономических, физических и других. Вне области экономики иногда называется также распределением Брэдфорда.

Определение

Пусть случайная величина $X\!$ такова, что её распределение задаётся равенством:

$F_X(x)=P(X<x) =1- \left(\frac{x_m}{x}\right)^{k},\; \forall x \ge x_m$,

где $x_m,k>0\!$. Тогда говорят, что $X\!$ имеет распределение Парето с параметрами $x_m\!$ и $k\!$. Плотность распределения Парето имеет вид:

$f_X(x) = \left\{ \begin{matrix} \frac{kx_m^k}{x^{k+1}}, & x \ge x_m \\ 0, & x < x_m \end{matrix} \right..$

Моменты

Моменты случайной величины, имеющей распределение Парето, задаются формулой:

$\mathbb{E}\left[X^n\right] = \frac{kx_m^n}{k-n}$,

откуда в частности:

$\mathbb{E}[X] = \frac{kx_m}{k-1}$,

$\mathrm{D}[X] = \left(\frac{x_m}{k-1}\right)^2 \frac{k}{k-2}$.

Приложения

Вилфредо Парето изначально использовал это распределение для описания распределения благосостояния, а также распределения дохода^[1]. Его правило 20 к 80 (которое гласит: 20 % популяции владеет 80 % богатства) однако зависит от конкретной величины k, и утверждается, что фактически встречаются существенные количественные отклонения, например, данные самого Парето по Британии в Cours d'économie politique говорят, что там примерно 30 % населения владеет 70 % общего дохода.

Распределение Парето встречается не только в экономике. Можно привести следующие примеры:

• В лингвистике распределение Парето известно под именем закона Ципфа (для разных языков показатель степени может несколько различаться, также существует небольшое отклонение от простой степенной зависимости у самых частотных слов, однако в целом степенной закон описывает это распределение достаточно хорошо). Частными проявлениями этой закономерности можно считать:
  • Зависимость абсолютной частоты слов (сколько всего раз каждое конкретное слово встретилось) в достаточно длинном тексте от ранга (порядкового номера при упорядочении слов по абсолютной частоте). Степенной характер остается вне зависимости от того, приводятся ли слова к начальной форме или берутся из текста как есть.
  • Аналогичная кривая для популярности имен.
• Распределение размера населенных пунктов.^[2]
• Распределение размера файла в интернет-траффике по TCP-протоколу.^[2]

См. также

• Закон Парето
• Кривая Парето
• Закон Ципфа

Примечания

1. ↑ Pareto, Vilfredo, Cours d’Économie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Geneva, 1964, pages 299—345.
2. ↑ ^{1 2} William J. Reed et al., «The Double Pareto-Lognormal Distribution — A New Parametric Model for Size Distributions», Communications in Statistics : Theory and Methods 33(8), 1733—1753, 2004 p 18 et seq.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула