- Непрерывное равномерное распределение
-
Непрерывное равномерное распределение Плотность вероятности
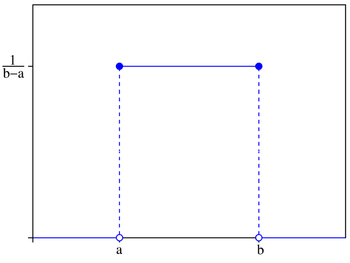
Функция распределения
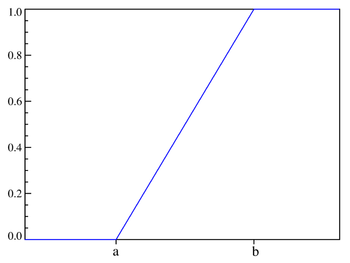
Обозначение 
Параметры  ,
,  — коэффициент сдвига,
— коэффициент сдвига,  — коэффициент масштаба
— коэффициент масштабаНоситель 
Плотность вероятности 
Функция распределения 
Математическое ожидание 
Медиана 
Мода любое число из отрезка ![[a,b]\!](52d4fce11e59f0395730bb90f9b239cc.png)
Дисперсия 
Коэффициент асимметрии 
Коэффициент эксцесса 
Информационная энтропия 
Производящая функция моментов 
Характеристическая функция 
Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.Содержание
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке
![[a,b]\!](52d4fce11e59f0395730bb90f9b239cc.png) , где
, где  , если её плотность
, если её плотность  имеет вид:
имеет вид:Пишут:
![X \sim U[a,b]](12cc87a67ce350e5ec7bef503d6b7950.png) . Иногда значения плотности в граничных точках
. Иногда значения плотности в граничных точках  и
и  меняют на другие, например
меняют на другие, например  или
или  . Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.
. Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка
![[a,b]\!](52d4fce11e59f0395730bb90f9b239cc.png) , то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
, то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство: .
.
Производящая функция моментов
Простым интегрированием получаем производящую функцию моментов:
 ,
,
откуда находим все интересующие моменты непрерывного равномерного распределения:
![\mathbb{E}\left[X\right] = \frac{a+b}{2}](5104caab9afc66791342c3c09fe300cf.png) ,
,
![\mathbb{E}\left[X^2\right] = \frac{a^2+ab+b^2}{3}](853444594f590343b617ee645ddd52a1.png) ,
,
![\operatorname{D}\left[X\right] = \frac{(b-a)^2}{12}](b49fd34c16f981fc41df8f93edfdaa8a.png) .
.
Вообще,
![\mathbb{E}\left[X^n\right] = \frac{1}{n+1}\sum\limits_{k=0}^n{a^k b^{n-k}}=\frac{b^{n+1}-a^{n+1}}{(b-a)(n+1)}](c0da850bf5748d76c4a770ed0d341a89.png) .
.
Стандартное равномерное распределение
Если
 и
и  , то есть
, то есть ![X \sim U[0,1]](6faa779b64905e81f39babd70fe5927b.png) , то такое непрерывное равномерное распределение называют стандартным.
, то такое непрерывное равномерное распределение называют стандартным.Имеет место элементарное утверждение:
- Если случайная величина
![X \sim U[0,1]](6faa779b64905e81f39babd70fe5927b.png) и
и  , то
, то ![Y \sim U[\min(a,b),\max(a,b)]\!](4d79386c592670584d5f640fd7c5b9da.png) .
.
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
См. также
Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma многомерное нормальное | копула Категория:- Непрерывные распределения
Wikimedia Foundation. 2010.

![f_X(x) = \left\{
\begin{matrix}
{1 \over b-a}, & x\in [a,b] \\
0, & x\not\in [a,b]
\end{matrix}
\right..](85d4b9e265864dbbef2c7621883a87df.png)
