- Биномиальное распределение
-
Биномиальное распределение Функция вероятности
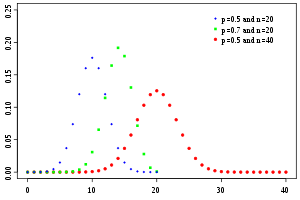
Функция распределения Обозначение 
Параметры  — число «испытаний»
— число «испытаний»
 — вероятность «успеха»
— вероятность «успеха»Носитель 
Функция вероятности 
Функция распределения 
Математическое ожидание 
Медиана одно из 
Мода 
Дисперсия 
Коэффициент асимметрии 
Коэффициент эксцесса 
Информационная энтропия 
Производящая функция моментов 
Характеристическая функция 
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна  .
.Содержание
Определение
Пусть
 — конечная последовательность независимых случайных величин с распределением Бернулли, то есть
— конечная последовательность независимых случайных величин с распределением Бернулли, то естьПостроим случайную величину
 :
: .
.
Тогда
 , число единиц (успехов) в последовательности
, число единиц (успехов) в последовательности  , имеет биномиальное распределение с
, имеет биномиальное распределение с  степенями свободы и вероятностью «успеха»
степенями свободы и вероятностью «успеха»  . Пишем:
. Пишем:  . Её функция вероятности задаётся формулой:
. Её функция вероятности задаётся формулой:где
 — биномиальный коэффициент.
— биномиальный коэффициент.Функция распределения
Функция распределения биномиального распределения может быть записана в виде суммы:
 ,
,
где
 обозначает наибольшее целое, не превосходящее число
обозначает наибольшее целое, не превосходящее число  , или в виде неполной бета-функции:
, или в виде неполной бета-функции: .
.
Моменты
Производящая функция моментов биномиального распределения имеет вид:
 ,
,
откуда
![\mathbb{E}[Y] = np](312a91b08bc6703d1c53c761b49ae9fe.png) ,
,![\mathbb{E}\left[Y^2\right] = np ( q + np )](9edb5ee63ebb158010e2ea9daf812261.png) ,
,
а дисперсия случайной величины.
![\mathbb{D}[Y] = npq](af20d0c8593f4695af97df834ad1563e.png) .
.
Свойства биномиального распределения
- Пусть
 и
и  . Тогда
. Тогда  .
. - Пусть
 и
и  . Тогда
. Тогда  .
.
Связь с другими распределениями
- Если
 , то, очевидно, получаем распределение Бернулли.
, то, очевидно, получаем распределение Бернулли. - Если
 большое, то в силу центральной предельной теоремы
большое, то в силу центральной предельной теоремы  , где
, где  — нормальное распределение с математическим ожиданием
— нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией  .
. - Если
 большое, а
большое, а  — фиксированное число, то
— фиксированное число, то  , где
, где  — распределение Пуассона с параметром
— распределение Пуассона с параметром  .
.
См. также
Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma многомерное нормальное | копула В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 12 мая 2011.Категория:- Дискретные распределения
Wikimedia Foundation. 2010.


