- Дискретное равномерное распределение
-
Дискретное равномерное распределение Функция вероятности
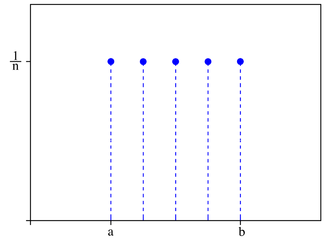
n=5, где n=b-a+1Функция распределения
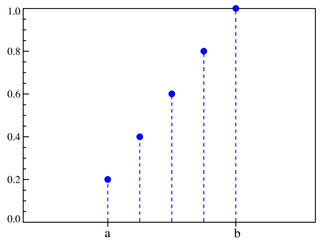
n=5, где n=b-a+1.Обозначение Параметры 


Носитель 
Функция вероятности 
Функция распределения 
Математическое ожидание 
Медиана 
Мода нет Дисперсия 
Коэффициент асимметрии 
Коэффициент эксцесса 
Информационная энтропия 
Производящая функция моментов 
Характеристическая функция 
В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.Примеры
- Случайная величина, принимающая значение
 , если выпал орёл, и
, если выпал орёл, и  , если выпала решка, имеет дискретное равномерное распределение. Она принимает оба значения с вероятностью 1/2.
, если выпала решка, имеет дискретное равномерное распределение. Она принимает оба значения с вероятностью 1/2. - Случайная величина, равная выпавшему числу на игральной кости, имеет дискретное равномерное распределение на
 , и она принимает каждое значение с вероятностью 1/6.
, и она принимает каждое значение с вероятностью 1/6.
Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma многомерное нормальное | копула Для улучшения этой статьи желательно?: - Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
- Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
Категория:- Дискретные распределения
- Случайная величина, принимающая значение
Wikimedia Foundation. 2010.
