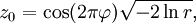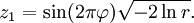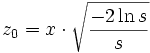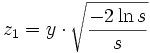Преобразование Бокса — Мюллера

Преобразование Бокса — Мюллера

Преобразование Бокса — Мюллера — метод моделирования стандартных нормально распределённых случайных величин. Имеет два варианта. Метод является точным, в отличие, например, от методов основывающихся на центральной предельной теореме.

Метод был опубликован в 1958 году Джорджем Боксом и Мервином Мюллером.

Первый вариант

Пусть r и 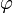$\varphi\$ — независимые случайные величины, равномерно распределённые на интервале (0, 1]. Вычислим z₀ и z₁ по формулам

$z_0 = \cos (2 \pi \varphi) \sqrt {-2 \ln r},$

$z_1 = \sin (2 \pi \varphi) \sqrt {-2 \ln r}.$

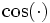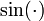Тогда z₀ и z₁ будут независимы и распределены нормально с математическим ожиданием 0 и дисперсией 1. При реализации на компьютере обычно быстрее не вычислять обе тригонометрические функции — $\cos (\cdot)$ и $\sin (\cdot)$ — а рассчитать одну из них через другую. Ещё лучше воспользоваться вместо этого вторым вариантом преобразования Бокса — Мюллера.

Второй вариант

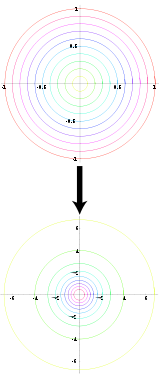
Пусть x и y — независимые случайные величины, равномерно распределённые на отрезке [−1, 1]. Вычислим s = R² = x² + y². Если окажется, что R > 1 или R = 0, то значения x и y следует «выбросить» и сгенерировать заново. Как только выполнится условие 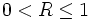$0 < R \le 1$, по формулам

$z_0 = x \cdot \sqrt {-2 \ln s \over s}$

и

$z_1 = y \cdot \sqrt {-2 \ln s \over s}$

следует рассчитать z₀ и z₁, которые, как и в первом случае, будут независимыми величинами, удовлетворяющими стандартному нормальному распределению.

Коэффициент использования базовых случайных величин для первого варианта, очевидно, равен единице. Для второго варианта это отношение площади окружности единичного радиуса к площади квадрата со стороной два, т. е. 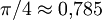$\pi / 4 \approx 0{,}785$. Тем не менее, на практике второй вариант обычно оказывается быстрее, за счёт того, что в нём используется только одна трансцендентная функция, 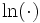$\ln (\cdot)$. Это преимущество для большинства реализаций перевешивает необходимость генерации большего числа равномерно распределённых случайных величин.

Переход к общему нормальному распределению

После получения стандартной нормальной случайной величины z, можно легко перейти к величине 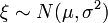$\xi \sim N (\mu, \sigma^2)$ распределённой нормально с математическим ожиданием μ и стандартным отклонением σ по формуле

ξ = μ + σz.

Это уже не является частью преобразования Бокса — Мюллера, но позволяет завершить генерацию нормальной случайной величины.