Геометрическое распределение

Геометрическое распределение, считающее неудачи

Функция вероятности
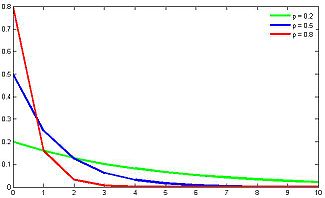
Функция распределения
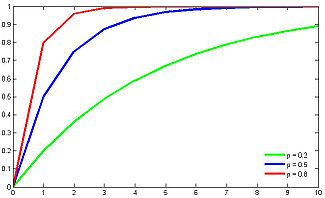
Обозначение
Параметры	$n \geq 0$ —уцы число «неудач» до магди как ты ле первого «успеха» $0\leq p \leq 1$ — вероятность «успеха» $\ q \equiv 1-p$ — вероятность «неудачи»
Носитель	$n \in \{0,1,2,3,\dots\}\!$
Функция вероятности	$q^n p\!$
Функция распределения	$1-q^n\!$
Математическое ожидание	$\frac{1}{p}$
Медиана	N/A
Мода	0
Дисперсия	$\frac{q}{p^2}$
Коэффициент асимметрии	$\frac{2-p}{\sqrt{1-p}}\!$
Коэффициент эксцесса	$6+\frac{p^2}{1-p}\!$
Информационная энтропия	$-\log_2 p-\frac{1-p}{p}\log_2\left({1-p}\right)\!$
Производящая функция моментов	$\frac{p}{1-qe^t}$
Характеристическая функция	$\frac{p}{1-qe^{it}}$

Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Определение

Пусть $X_1 ,\ldots, X_n,\ldots$ — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть

$X_i = \left\{ \begin{matrix} 1, & p \\ 0, & q \equiv 1-p \end{matrix} \right.,\; i=1,2,\ldots$

Построим случайную величину $Y = \min \left\{ i \mid X_i = 1 \right\} - 1$ — количество «неудач» до первого «успеха». Распределение случайной величины $Y$ называется геометрическим с вероятностью «успеха» $p$, что обозначается следующим образом: $Y \sim \mathrm{Geom}(p)$.

Функция вероятности случайной величины $Y$ имеет вид:

$\mathbb{P}(Y = n) = q^n p,\; n=0,1,2,\ldots$

Замечание

• Иногда полагают по определению, что $X$ — номер первого «успеха». Тогда функция вероятности принимает форму $\mathbb{P}(X = n) = q^{n-1} p$. В этом случае все формулы из таблицы справа должны быть модифицированы очевидным образом.
• Функция вероятности является геометрической прогрессией, откуда и происходит название распределения.

Моменты

Производящая функция моментов геометрического распределения имеет вид:

$M_Y(t) = \frac{p}{1-qe^t}$,

откуда

$\mathbb{E}[Y] = \frac{1}{p}$,

$\mathrm{D}[Y] = \frac{q}{p^2}$.

Свойства геометрического распределения

• Из всех дискретных распределений с фиксированным средним $\mu >1$ геометрическое распределение $\mathrm{Geom}(1/\mu)$ является одним из распределений с максимальной информационной энтропией.
• Если $Y_1,\ldots, Y_n$ независимы и $Y_i \sim \mathrm{Geom}(p_i),\; i=1,\ldots,n$, то

$Y = \min\limits_i (Y_i) \sim \mathrm{Geom}\left(1 - \prod\limits_{i=1}^n (1-p_i)\right)$.

• Геометрическое распределение бесконечно делимо.

Отсутствие памяти

Если $Y\sim \mathrm{Geom}(p)$, то $\mathbb{P}(X > m + n \mid X > m ) = \mathbb{P}(X>n)\;, \forall m,n \in \mathbb{N}\cup \{0\}$, то есть количество прошлых «неудач» не влияет на количество будущих «неудач».

Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти.

Связь с другими распределениями

• Геометрическое распределение является частным случаем отрицательного биномиального распределения: $\mathrm{Geom}(p) \equiv \mathrm{NB}(1,p)$.
• Если $Y_1,\ldots, Y_n$ независимы и $Y_i \sim \mathrm{Geom}(p),\; i=1,\ldots,n$, то

$\sum\limits_{i=1}^n Y_i \sim \mathrm{NB}(n,p)$.

Пример

Пусть игральная кость выбрасывается до выпадания первой «шестёрки». Тогда вероятность, что нам потребуется не больше трёх вбросов равна:

$\mathbb{P}(Y \le 2) = \mathbb{P}(Y=0) + \mathbb{P}(Y = 1) + \mathbb{P}(Y=2) =$

$= \left(\frac{5}{6}\right)^0 \left(\frac{1}{6}\right) + \left(\frac{5}{6}\right)^1 \left(\frac{1}{6}\right) + \left(\frac{5}{6}\right)^2 \left(\frac{1}{6}\right) \approx 0,42$.

Ожидаемое число бросков равно:

$\mathbb{E}[Y] + 1 = \frac{5/6}{1/6} + 1 = 6$.

См. также

• Биномиальное распределение.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула

Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации. Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.