БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

распределение Бернулли,- распределение вероятностей случайной величины X, принимающей целочисленные значения с вероятностями соответственно

( - биномиальный коэффициент; р- параметр Б. р., наз. вероятностью положительного исхода, принимающей значения на отрезке ). Б. р.- одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Пусть - последовательность независимых случайных величин, каждая из к-рых может принимать лишь два значения 1 или 0 с вероятностями ри 1 - р соответственно (т. е. каждая из подчиняется Б. р. при n=1). Величины можно трактовать как результаты независимых испытаний, причем в случав "положительного исхода" и в случае "отрицательного исхода" испытания с номером г. Если общее количество независимых испытаний пфиксировапно, то такая схема на:;. Бернулли испытаниями, причем суммарное количество положительных исходов

в этом случае подчиняется Б. р. с параметром р.

Математич. ожидание 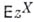(производящая функция Б. <р.) при любом значении zесть многочлен 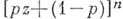, представление к-рого по формуле бинома Ньютона имеет вид , (отсюда и произошло само назв. "Б. р."). Моменты Б. р. выражаются формулами

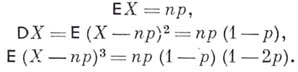
Функция Б. р. определяется при любом действительном значении формулой

где [у]-целая часть у, причем

(В ( а, b) - бета-функция Эйлера, интеграл в правой части наз. неполной бета-функцией).

При функция Б. р. выражается в терминах функции Ф стандартного нормального распределения асимптотич. формулой (теорема Муавра - Лапласа)

^где

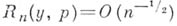
равномерно для всех действительных у. Существуют и другие нормальные приближения Б. р. с остатками более высокого порядка малости.

Если количество независимых испытаний пвелико, а вероятность рмала, то индивидуальные вероятности приближенно выражаются в терминах Пуассона распределения:

При этом, если 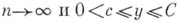(с и С - постоянные), то равномерно относительно всех риз интервала имеет место асимптотич. формула

где .

Многомерным обобщением Б. р. является полиномиальное распределение.

Лит.:[1] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; [2] Феллер В., Введение в теорию вероятностей и её приложения, пер. с англ., 2 изд., М., 1967; [3] Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973; [4] Прохоров Ю. В., "Успехи математических наук", 1953, т. 8, №3, с. 135-42; 15] Большее Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968. Л. Н. Большее.