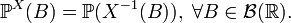Распределения вероятностей

Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.

Определение

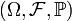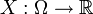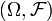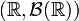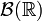Определение 1. Пусть задано вероятностное пространство $(\Omega, \mathcal{F}, \mathbb{P})$, и на нём определена случайная величина $X:\Omega \to \mathbb{R}$. В частности, по определению, X является измеримым отображением измеримого пространства $(\Omega, \mathcal{F})$ в измеримое пространство $(\mathbb{R},\mathcal{B}(\mathbb{R}))$, где $\mathcal{B}(\mathbb{R})$ обозначает борелевскую сигма-алгебру на $\mathbb{R}$. Тогда случайная величина X индуцирует вероятностную меру $\mathbb{P}^X$ на $\mathbb{R}$ следующим образом:

$\mathbb{P}^X(B) = \mathbb{P}(X^{-1}(B)),\; \forall B\in \mathcal{B}(\mathbb{R}).$

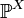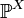Мера $\mathbb{P}^X$ называется распределением случайной величины X.

Способы задания распределений

Определение 2. Функция $F_X(x) = \mathbb{P}^X((-\infty,x]) = \mathbb{P}(X \leqslant x)$ называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает

Теорема 1. Функция распределения F_X(x) любой случайной величины удовлетворяет следующим трем свойствам:

1. F_X - функция неубывающая;
2. $\lim_{x\to -\infty} F_X(x) = 0,\; \lim_{x\to \infty}F_X(x) = 1$;
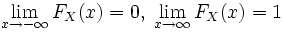3. F_X непрерывна справа.

Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида $\{(-\infty,x]\}_{x\in \mathbb{R}}$, вытекает

Теорема 2. Любая функция F(x), удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения $\mathbb{P}^X$.

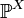Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.

Дискретные распределения

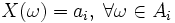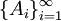Определение 2. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть $X(\omega) = a_i,\; \forall \omega \in A_i$, где $\{A_i\}_{i=1}^{\infty}$ - разбиение Ω.

Распределение простой случайной величины тогда по определению задаётся: 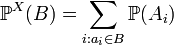$\mathbb{P}^X(B) = \sum_{i:a_i \in B} \mathbb{P}(A_i)$. Введя обозначение 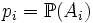$p_i = \mathbb{P}(A_i)$, можно задать функцию p(a_i) = p_i. Очевидно, что 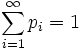$\sum_{i=1}^{\infty}p_i = 1$. Используя счётную аддитивность 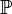$\mathbb{P}$, легко показать, что эта функция однозначно определяет распределение X.

Определение 3. Функция p(a_i) = p_i, где 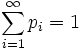$\sum_{i=1}^{\infty} p_i = 1$ часто называется дискретным распределением.

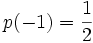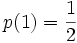Пример 1. Пусть функция p задана таким образом, что $p(-1) = \frac{1}{2}$ и $p(1) = \frac{1}{2}$. Эта функция задаёт распределение случайной величины X такой, что $\mathbb{P}(X=\pm 1) = \frac{1}{2}$.

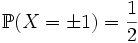Теорема 3. Дискретное распределение обладает следующими свойствами:

1. $p_i \geqslant 0$;

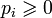2. ∑	pi = 1
   i

   .

Непрерывные распределения

Непрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть смесь дискретного и непрерывного.

Абсолютно непрерывные распределения

Основная статья: Плотность вероятности

Определение 4. Распределение случайной величины X называется абсолютно непрерывным, если существует неотрицательная функция 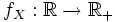$f_X:\mathbb{R}\to \mathbb{R}_+$, такая что 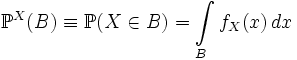$\mathbb{P}^X(B) \equiv \mathbb{P}(X\in B) = \int\limits_B f_X(x)\, dx$. Функция f_X тогда называется плотностью распределения случайной величины X.

Пример 2. Пусть f(x) = 1, когда 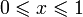$0\leqslant x \leqslant 1$, и 0 иначе. Тогда 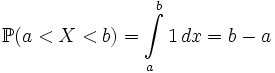$\mathbb{P}(a < X < b) = \int\limits_a^b 1\, dx = b-a$, если $(a,b) \subset [0,1]$.

Очевидно, что для любой плотности распределения f_X верно равенство 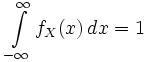$\int\limits_{-\infty}^{\infty} f_X(x)\, dx = 1$. Верна и обратная

Теорема 4. Если функция 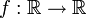$f:\mathbb{R}\to \mathbb{R}$ такая, что:

1. $f(x) \geqslant 0,\; \forall x \in \mathbb{R}$;
2. $\int\limits_{-\infty}^{\infty} f(x)\, dx = 1$,

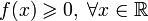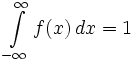то существует распределение 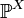$\mathbb{P}^X$ такое, что f(x) является его плотностью.

Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.

Теорема 5. Если f(x) — непрерывная плотность распределения, а F(x) — его кумулятивная функция, то

1. $F'(x) = f(x),\; \forall x \in \mathbb{R},$
2. $F(x) = \int\limits_{-\infty}^x f(t)\, dt$.

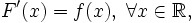
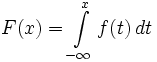Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править