- Кумулятивная функция распределения
-
Кумуляти́вная фу́нкция распределе́ния (или просто функция распределения) в теории вероятностей однозначно задаёт распределение случайной величины или случайного вектора.
Содержание
Определение
Пусть дано вероятностное пространство
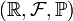 , и на нём определена случайная величина X с распределением
, и на нём определена случайная величина X с распределением 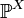 . Тогда функцией распределения случайной величины X называется функция
. Тогда функцией распределения случайной величины X называется функция ![F_X\colon\mathbb{R} \to [0,1]](/pictures/wiki/files/48/01e0d468d8996bae434f2e507b042749.png) , задаваемая формулой:
, задаваемая формулой:![F_X(x) = \mathbb{P}( X \leqslant x ) \equiv \mathbb{P}^X\left((-\infty, x]\right)](/pictures/wiki/files/53/5280c7af4feaad80158322157422453e.png) .
.
Свойства
- FX не убывает на всей числовой прямой.
- FX непрерывна справа.
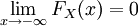 .
.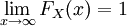 .
.
- Распределение случайной величины
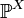 однозначно определяет функцию распределения.
однозначно определяет функцию распределения.
- Верно и обратное: если функция F(x) удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что F(x) является её функцией распределения.
- По определению непрерывности справа, функция FX имеет правый предел FX(x + ) в любой точке
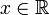 , и он совпадает со значением функции FX(x) в этой точке.
, и он совпадает со значением функции FX(x) в этой точке.
- В силу неубывания, функция FX также имеет и левый предел FX(x − ) в любой точке
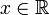 , который может не совпадать со значением функции. Таким образом, функция FX либо непрерывна в точке, либо имеет в ней разрыв первого рода.
, который может не совпадать со значением функции. Таким образом, функция FX либо непрерывна в точке, либо имеет в ней разрыв первого рода.
- В силу неубывания, функция FX также имеет и левый предел FX(x − ) в любой точке
Тождества
Из свойств вероятности следует, что
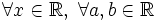 , таких что a < b:
, таких что a < b: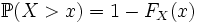 ;
;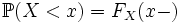 ;
;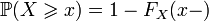 ;
;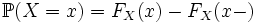 ;
;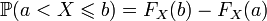 ;
;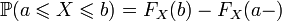 ;
;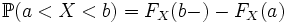 ;
;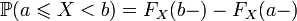 .
.
Дискретные распределения
Если случайная величина X дискретна, то есть её распределение однозначно задаётся функцией вероятности
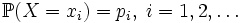 ,
,
то функция распределения FX этой случайной величины кусочно-постоянна и может быть записана как:
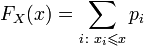 .
.
Эта функция непрерывна в любой точке
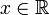 , такой что
, такой что 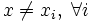 , и имеет разрыв, равный pi, в x = xi.
, и имеет разрыв, равный pi, в x = xi.Непрерывные распределения
Распределение
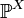 называется непрерывным, если такова его функция распределения FX. В этом случае:
называется непрерывным, если такова его функция распределения FX. В этом случае: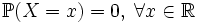 ,
,
и
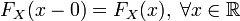 ,
,
а следовательно формулы имеют вид:
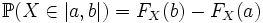 ,
,
где | a,b | означает любой интервал, открытый или закрытый, конечный или бесконечный.
Абсолютно непрерывные распределения
Распределение
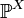 называется абсолютно непрерывным, если существует неотрицательная почти всюду (относительно меры Лебега) функция fX(x), такая что:
называется абсолютно непрерывным, если существует неотрицательная почти всюду (относительно меры Лебега) функция fX(x), такая что: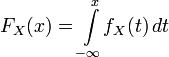 .
.
Функция fX называется плотностью распределения. Известно, что функция абсолютно непрерывного распределения непрерывна, и более того если
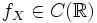 , то
, то 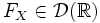 , и
, и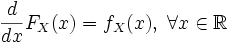 .
.
Вариации и обобщения
Многомерные функции распределения
Пусть
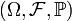 фиксированное вероятностное пространство, и
фиксированное вероятностное пространство, и 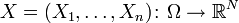 — случайный вектор. Тогда распределение
— случайный вектор. Тогда распределение 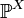 является вероятностной мерой на
является вероятностной мерой на  . Функция этого распределения
. Функция этого распределения ![F_X\colon\mathbb{R}^n \to [0,1]](/pictures/wiki/files/97/aba8cc6b6ed8c9ddc8ece48ba4daf7d6.png) задаётся по определению следующим образом:
задаётся по определению следующим образом:![F_X(x_1,\ldots,x_n) = \mathbb{P}(X_1 \leqslant x_1 ,\ldots, X_n \leqslant x_n) \equiv \mathbb{P}^X \left(\prod\limits_{i=1}^n (-\infty,x_i]\right)](/pictures/wiki/files/101/e5bd01f71ba29d76020e88c9c69392ad.png) ,
,
где
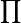 в данном случае обозначает декартово произведение множеств.
в данном случае обозначает декартово произведение множеств.Свойства многомерных функций распределения аналогичны одномерному случаю. Также сохраняется взаимно-однозначное соответствие между распределениями на
 и многомерными функциями распределения. Однако, формулы для вычисления вероятностей существенно усложняются, и потому функции распределения редко используются для n > 1.
и многомерными функциями распределения. Однако, формулы для вычисления вероятностей существенно усложняются, и потому функции распределения редко используются для n > 1.См. также
Wikimedia Foundation. 2010.
