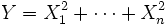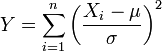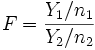- Хи-квадрат распределение
-
Распределение хи-квадрат Плотность вероятности
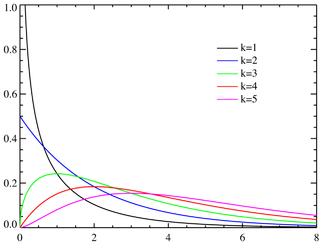
k - число степеней свободыФункция распределения

k - число степеней свободыПараметры 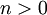 число степеней свободы
число степеней свободыНоситель 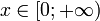
Плотность вероятности 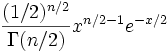
Функция распределения 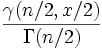
Математическое ожидание 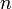
Медиана примерно 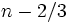
Мода 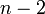 если
если 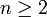
Дисперсия 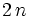
Коэффициент асимметрии 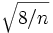
Коэффициент эксцесса 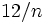
Информационная энтропия ![\frac{n}{2}\!+\!\ln\left[2\Gamma\left({n \over 2}\right)\right]\!+\!\left(1\!-\!\frac{n}{2}\right)\psi\left(\frac{n}{2}\right)](/pictures/wiki/files/102/fdac2603739bb8ef87771f1666c260e9.png)
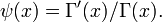
Производящая функция моментов 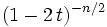 , если
, если 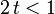
Характеристическая функция 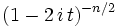
Распределение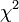 (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных случайных величин.
(хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных случайных величин.Содержание
Определение
Пусть
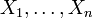 — совместно независимые стандартные нормальные случайные величины, то есть:
— совместно независимые стандартные нормальные случайные величины, то есть: 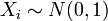 . Тогда случайная величина
. Тогда случайная величинаимеет распределение хи-квадрат с n степенями свободы, обозначаемое
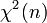 .
.Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
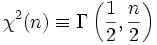 .
.
Следовательно, плотность распределения хи-квадрат имеет вид
 ,
,
а его функция распределения
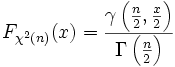 ,
,
где
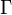 и
и 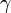 обозначают соответственно полную и неполную гамма-функции.
обозначают соответственно полную и неполную гамма-функции.Свойства распределения хи-квадрат
- Распределение хи-квадрат устойчиво относительно суммирования. Если
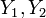 независимы, и
независимы, и 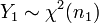 , а
, а 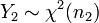 , то
, то
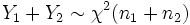 .
.
- Из определения легко получить моменты распределения хи-квадрат. Если
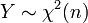 , то
, то
![\mathbb{E}[Y] = n](/pictures/wiki/files/101/e06f94e23c8fd23f951c3a30db4dbc74.png) ,
,![\!\mathrm{D}[Y] = 2n](/pictures/wiki/files/98/b711592e2381d63f19f315552ef8bfe6.png) .
.
- В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины
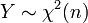 может быть приближено нормальным
может быть приближено нормальным 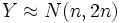 . Более точно
. Более точно
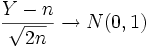 по распределению при
по распределению при 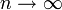 .
.
Связь с другими распределениями
- Если
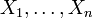 независимые нормальные случайные величины, то есть:
независимые нормальные случайные величины, то есть: 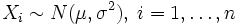 , то случайная величина
, то случайная величина
имеет распределение хи-квадрат.
- Если
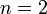 , то распределение хи-квадрат совпадает с экспоненциальным распределением:
, то распределение хи-квадрат совпадает с экспоненциальным распределением:
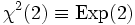 .
.
- Если
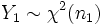 и
и 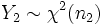 , то случайная величина
, то случайная величина
имеет распределение Фишера со степенями свободы
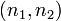 .
.Процентили
Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное править
Wikimedia Foundation. 2010.