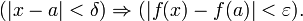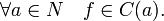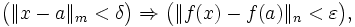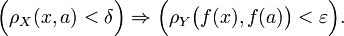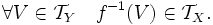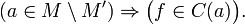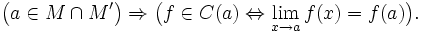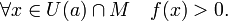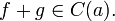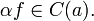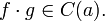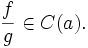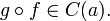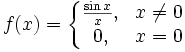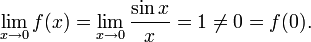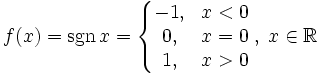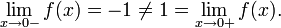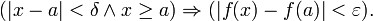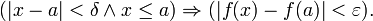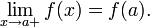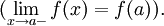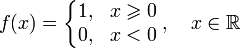- Разрыв первого рода
-
Непреры́вное отображе́ние или непрерывная функция — это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения.
Это понятие определятся немного по-разному в различных разделах математики; наиболее общее определение используется в общей топологии.
Содержание
Определения
Непрерывная числовая функция
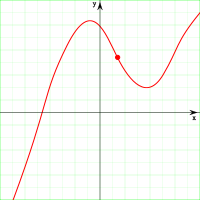
- Пусть дана функция
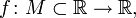 и
и 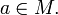 Тогда говорят, что f непрерывна в точке a и пишут
Тогда говорят, что f непрерывна в точке a и пишут 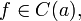 если
если 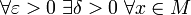
- Пусть дано подмножество
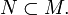 Тогда говорят, что f непрерывна на N и пишут
Тогда говорят, что f непрерывна на N и пишут 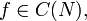 если
если
Непрерывное отображение из Rm в Rn
Обобщая одномерный случай, функция
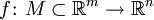 называется непрерывной в точке
называется непрерывной в точке 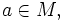 если
если 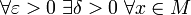
где
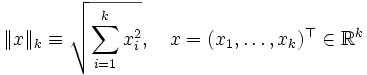 — евклидова норма в
— евклидова норма в 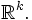
Непрерывное отображение метрических пространств
В предыдущем определении наличие операции вычитания, точнее линейной структуры, в евклидовых пространствах не играет принципиальной роли. Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение
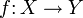 метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если
метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если 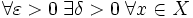
Непрерывное отображение топологических пространств
В предыдущих определениях важно не наличие точной меры расстояния, а лишь понятия близости. Непрерывное отображение переводит близкие точки в близкие. Множество, в котором указан некоторый набор подмножеств
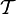 , позволяющий говорить о близких точках, называется топологическим пространством. Отображение
, позволяющий говорить о близких точках, называется топологическим пространством. Отображение 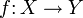 топологического пространства
топологического пространства 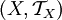 в топологическое пространство
в топологическое пространство 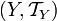 называется непрерывным, если прообраз любого открытого множества открыт:
называется непрерывным, если прообраз любого открытого множества открыт:Связанные определения
Если функция не является непрерывной в точке a, то говорят, что она в ней разры́вна и пишут
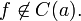 Согласно замечанию выше функция может быть разрывной только в предельной точке области определения, и справедливо одно из двух:
Согласно замечанию выше функция может быть разрывной только в предельной точке области определения, и справедливо одно из двух:- Либо предел
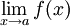 не существует;
не существует; - Либо он существует, но
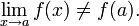
Пусть существует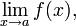 но
но 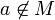 или
или 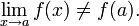 Тогда a называется то́чкой устрани́мого разры́ва. Положив
Тогда a называется то́чкой устрани́мого разры́ва. Положив 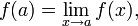 можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.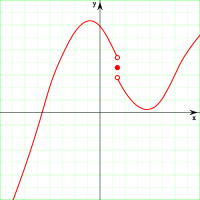
Пусть не сущестует двусторонний предел
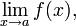 но существуют конечные (и различные) односторонние пределы
но существуют конечные (и различные) односторонние пределы 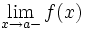 и
и 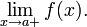 Тогда
Тогда 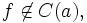 и a называется то́чкой разры́ва пе́рвого ро́да.
и a называется то́чкой разры́ва пе́рвого ро́да.Если
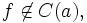 и a не является точкой устранимого разрыва или разрыва первого рода, то есть хотя бы один односторонний предел не существует или бесконечен, то она называется то́чкой разры́ва второ́го ро́да.
и a не является точкой устранимого разрыва или разрыва первого рода, то есть хотя бы один односторонний предел не существует или бесконечен, то она называется то́чкой разры́ва второ́го ро́да.Свойства
- Функция всегда непрерывна в изолированной точке области определения, то есть
- В предельной точке области определения непрерывность функции эквивалентна существованию предела, равного значению функции в точке:
Вещественнозначаные функции
- Функция сохраняет знак в окрестности точки непрерывности. Пусть
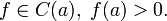 Тогда существует окрестность U(a) такая, что
Тогда существует окрестность U(a) такая, что
- Сумма непрерывных функций также является непрерывной. Пусть
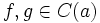 . Тогда
. Тогда
- Непрерывная функция умноженная на константу также является непрерывной. Пусть
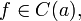 и
и 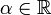 — произвольная константа. Тогда
— произвольная константа. Тогда
- Произведение непрерывных функций также является непрерывным. Пусть
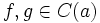 . Тогда
. Тогда
- Частное непрерывных функций также является непрерывным. Пусть
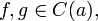 и
и 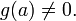 Тогда существует окрестность U(a), в которой функция
Тогда существует окрестность U(a), в которой функция 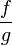 определена, и
определена, и
- Композиция двух непрерывных функций так же является непрерывной. Пусть
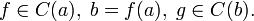 Тогда
Тогда
- Дифференцируемая функция всегда непрерывна. Обратное, вообще говоря, неверно. Например, функция Ван-дер-Вардена непрерывна, но не дифференцируема на всей прямой.
- Теорема Больцано — Коши;
- Теорема Вейерштрасса о функции, непрерывной на компакте.
Примеры
- Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические прямые и обратные функции непрерывны везде в своей области определения.
- Функция
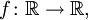 задаваемая формулой
задаваемая формулой
непрерывна в любой точке
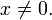 Точка x = 0 является точкой устранимого разрыва, ибо
Точка x = 0 является точкой устранимого разрыва, ибонепрерывна в любом
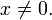 Точка x = 0 является точкой разрыва первого рода, ибо
Точка x = 0 является точкой разрыва первого рода, ибонепрерывна в любом
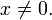
Вариации и бобщения
Односторнняя непрерывность
- Пусть дана функция
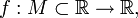 и
и 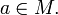 Тогда говорят, что f непреры́вна спра́ва в точке a, если
Тогда говорят, что f непреры́вна спра́ва в точке a, если 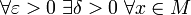
- Говорят, что f непреры́вна сле́ва в точке a, если
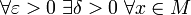
Замечания
- Функция непрерывна тогда и только тогда, когда она непрерывна одновременно справа и слева.
- Функция непрерывна справа в предельной точке области определения тогда и только тогда, когда существует правосторонний предел
- Функция непрерывна слева в предельной точке области определения тогда и только тогда, когда существует левосторонний предел
- Все базовые свойства непрерывных функций переносятся на односторонне непрерывные функции.
Примеры
- Функция
непрерывна справа (но не слева) в точке x = 0. Во всех других точках она непрерывна.
- Кумулятивная функция распределения дискретной случайной величины в теории вероятностей непрерывна справа в любой точке.
См. также
- Пусть дана функция
Wikimedia Foundation. 2010.