- Теорема Вейерштрасса о функции, непрерывной на компакте
-
Теоре́ма Вейерштра́сса в математическом анализе и общей топологии гласит, что функция, непрерывная на компактe, ограничена на нём и достигает своей верхней и нижней грани.
Содержание
Формулировка
Пусть дана непрерывная числовая функция, определённая на отрезке, то есть
![f:[a,\;b] \to \mathbb{R}](/pictures/wiki/files/56/8ca38b0c1c0c11faa70db123c003df63.png) и
и ![f\in C\bigl( [a,\;b] \bigr).](/pictures/wiki/files/98/b3710d3d3c864ceb5b8148ed402f630c.png) Пусть
Пусть— точные верхняя и нижняя грани множества значений функции f соответственно. Тогда
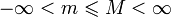 и существуют
и существуют ![x_m,\;x_M \in [a,\;b]](/pictures/wiki/files/99/cd41debb8684274988c14779b8332ef9.png) такие, что
такие, что
Доказательство для R
Пусть f(x) — функция, отвечающая условиям теоремы (на компакте A), 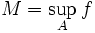 . Возьмём последовательность чисел am таких, что
. Возьмём последовательность чисел am таких, что 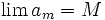 и am < M. Для каждого m найдётся точка xm, такая что am < f(xm). Имеем дело с компактом, поэтому, согласно теореме Больцана — Вейерштрасса из последовательности xm можно выделить сходящуюся последовательность
и am < M. Для каждого m найдётся точка xm, такая что am < f(xm). Имеем дело с компактом, поэтому, согласно теореме Больцана — Вейерштрасса из последовательности xm можно выделить сходящуюся последовательность 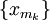 , предел которой лежит в A.
, предел которой лежит в A.
Для любого xm справедливо 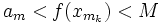 , поэтому, применяя предельный переход, получаем
, поэтому, применяя предельный переход, получаем 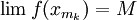 и в силу непрерывности функции существует точка x0 такая, что
и в силу непрерывности функции существует точка x0 такая, что 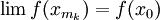 и, следовательно M = f(x0).
и, следовательно M = f(x0).
Таким образом функция f(x) ограничена и достигает своей верхней грани при x = x0. Аналогично и для нижней грани.

![M = \sup\limits_{x\in [a,\;b]}f(x),\quad m = \inf\limits_{x\in [a,\;b]} f(x)](/pictures/wiki/files/102/fdbfb4ea25d725db988f879c13637557.png)

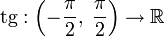
![f:[a,\;b] \to \R](/pictures/wiki/files/50/2830b6fe9eff0e32947481220609285c.png)
![M = \sup\limits_{x\in [a,\;b]}f(x) &lt; +\infty](/pictures/wiki/files/98/ba287951cc56c610b606bc69fb2875b6.png) и
и ![\exists x_M \in [a,\;b] : f(x_M) = M.](/pictures/wiki/files/51/3cc832e7bdc5b73794720bb617604b69.png)
![m = \inf\limits_{x\in [a,\;b]}f(x) &gt; -\infty](/pictures/wiki/files/102/f0217465d00f83339f0e38f79b429d66.png) и
и ![\exists x_m \in [a,\;b] : f(x_m) = m.](/pictures/wiki/files/97/ad4e96dada1e5962f447122fed6cf698.png)
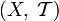 и
и 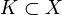 . Пусть дана непрерывная функция
. Пусть дана непрерывная функция 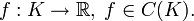 Тогда
Тогда![-\infty &lt; m \equiv \inf\limits_{x\in [a,\;b]} f(x) \leqslant M \equiv \sup\limits_{x\in [a,\;b]}f(x) &lt; +\infty](/pictures/wiki/files/101/e889cdadb582d15a01e070268c1d3d1e.png)