Пуассона распределение

Распределение Пуассона

Функция вероятности
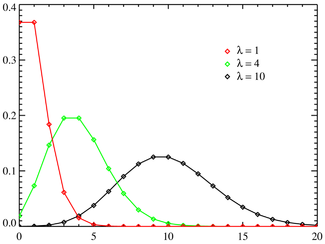
Функция распределения
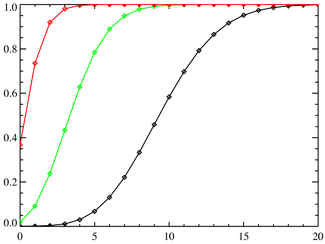
Параметры	$\lambda \in (0,\infty)$
Носитель	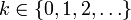$k \in \{0,1,2,\ldots\}$
Функция вероятности	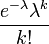$\frac{e^{-\lambda} \lambda^k}{k!}\!$
Функция распределения	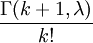$\frac{\Gamma(k+1, \lambda)}{k!}\!$
Математическое ожидание	$\lambda\,$
Медиана	N/A
Мода	$\lfloor\lambda\rfloor$
Дисперсия	$\lambda\,$
Коэффициент асимметрии	$\lambda^{-1/2}\,$
Коэффициент эксцесса	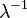$\lambda^{-1}\,$
Информационная энтропия	$\lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}$
Производящая функция моментов	$\exp(\lambda (e^t-1))\,$
Характеристическая функция	$\exp(\lambda (e^{it}-1))\,$

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в Теории массового обслуживания.

Определение

Выберем фиксированное число λ > 0 и определим дискретное распределение, задаваемое следующей функцией вероятности:

$p(k) \equiv \mathbb{P}(Y=k) = \frac{\lambda^k}{k!}\, e^{-\lambda}$,

где

• k! обозначает факториал,
• $e = 2.718281828\ldots$ — основание натурального логарифма.

Тот факт, что случайная величина Y имеет распределение Пуассона с параметром λ, записывается: $Y \sim~ \mathrm{P}(\lambda)$.

Моменты

Производящая функция моментов распределения Пуассона имеет вид:

$E_Y(t) = e^{\lambda \left(e^t -1\right)}$,

откуда

$\mathbb{M}[Y] = \lambda$,

$\mathbb{D}[Y] = \lambda$.

Свойства распределения Пуассона

• Сумма независимых пуассоновских случайных величин, также имеет распределение Пуассона. Пусть $Y_i \sim \mathrm{P}(\lambda_i),\; i=1,\ldots,n$. Тогда

$Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right)$.

• Пусть $Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2$, и Y = Y₁ + Y₂. Тогда условное распределение Y₁ при условии, что Y = y, биномиально. Более точно:

$Y_1\mid Y = y \sim \mathrm{mrBin}\left(y, \frac{\lambda_1}{\lambda_1+\lambda_2}\right)$.

См. также

• Биномиальное распределение;
• Пуассон, Симеон Дени.

Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править