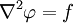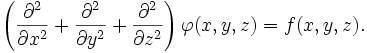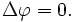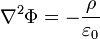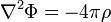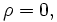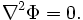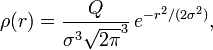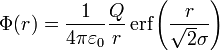- Пуассона уравнение
-
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает
- электростатическое поле,
- стационарное поле температуры,
- поле давления,
- поле потенциала скорости в гидродинамике.
Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.
Это уравнение имеет вид:
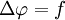
где Δ — оператор Лапласа или лапласиан, а f — действительная или комплексная функция на некотором многообразии. Когда в качестве многообразия выступает Евклидово пространство, оператор Лапласа часто обозначается как
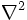 и уравнение Пуассона принимает вид:
и уравнение Пуассона принимает вид:В трёхмерной декартовой системе координат уравнение принимает форму:
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».
Содержание
Электростатика
Уравнение Пуассона является одним из краеугольных камней электростатики. Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:
где
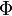 — электростатический потенциал (в вольтах),
— электростатический потенциал (в вольтах), 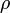 — объёмная плотность заряда (в кулонах на кубический метр), а
— объёмная плотность заряда (в кулонах на кубический метр), а 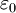 — диэлектрическая проницаемость вакуума (в фарадах на метр).
— диэлектрическая проницаемость вакуума (в фарадах на метр).В единицах системы СГС:
В области пространства, где нет непарной плотности заряда, имеем:
и уравнение для потенциала превращается в уравнение Лапласа:
Потенциал гауссовой объёмной плотности заряда
Если мы имеем объёмную сферически симметричную плотность гауссового распределения заряда ρ(r):
где Q — общий заряд, тогда решение Φ (r) уравнения Пуассона:
даётся:
где erf(x) — функция ошибок. Это решение может быть проверено напрямую вычислением
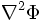 . Заметьте, что для r, много больших, чем σ, erf(x) приближается к единице, и потенциал Φ (r) приближается к потенциалу точечного заряда
. Заметьте, что для r, много больших, чем σ, erf(x) приближается к единице, и потенциал Φ (r) приближается к потенциалу точечного заряда 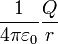 , как и можно было ожидать.
, как и можно было ожидать.См. также
- Дискретное уравнение Пуассона
- Экранированное уравнение Пуассона
Ссылки
- Poisson Equation at EqWorld: The World of Mathematical Equations.
- L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
Wikimedia Foundation. 2010.