- Теорема Брахмагупты
-
Теоре́ма Брахмагу́пты — теорема элементарной геометрии, найденная в седьмом столетии нашей эры индийским математиком Брахмагуптой. Приведём её вместе с доказательством.
Если вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке
 , то прямая, проходящая через точку
, то прямая, проходящая через точку  и перпендикулярная одной из его сторон, делит противоположную ей сторону пополам.
и перпендикулярная одной из его сторон, делит противоположную ей сторону пополам.Доказательство
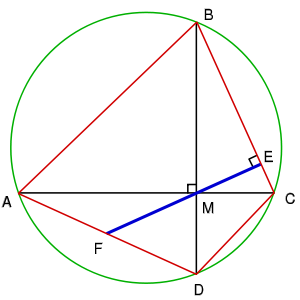
На рисунке изображён вписанный четырёхугольник
 , имеющий перпендикулярные диагонали
, имеющий перпендикулярные диагонали  и
и  , а прямая
, а прямая  перпендикулярна стороне
перпендикулярна стороне  и пересекает сторону
и пересекает сторону  в точке
в точке  . Тогда
. Тогда  Следовательно, треугольник
Следовательно, треугольник  — равнобедренный. Аналогично, равнобедренным будет и треугольник
— равнобедренный. Аналогично, равнобедренным будет и треугольник  . Поэтому
. Поэтому  .
.Ссылки
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
Многоугольники По числу вершин 1-10 Одноугольник • Двуугольник • Треугольник • Четырёхугольник (Дельтоид) • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник 11-20 Одиннадцатиугольник (англ.) • Двенадцатиугольник Правильные Выпуклые Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • ... • 17-угольник • ... • 257-угольник • ... • 65537-угольник Звёздчатая форма Звезды (Пентаграмма • Гексаграмма • Октаграмма) Выпуклые Четырёхугольники: Параллелограмм • Прямоугольник • Ромб • Трапеция
ПланигонСм. также Теория и практика: Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника Категории:- Многоугольники
- Теоремы
- Планиметрия
Wikimedia Foundation. 2010.