Правильный шестиугольник

Правильный шестиугольник

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Свойства

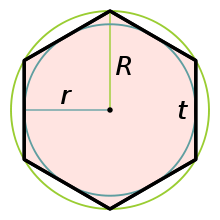
• Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности ($R = t$), поскольку $2 \sin \frac{\pi}{6} = 1$.
• Все углы равны 120°.
• Радиус вписанной окружности равен:

  $r = \frac{\sqrt 3}{2} R = \frac{\sqrt 3}{2} t$

• Периметр правильного шестиугольника равен:

  $P = 6 R = 4 \sqrt 3 r$

• Площадь правильного шестиугольника рассчитывается по формулам:

  $S = \frac{3 \sqrt 3}{2} R^2 = \frac{3 \sqrt 3}{2} t^2$

  $S = 2 \sqrt 3 r^2$

• Шестиугольники замещают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
• Правильный шестиугольник со стороной $\frac{1}{\sqrt 3}$ является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной $\frac{1}{\sqrt 3}$ (лемма Пала)^[1].

Построение

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Правильный шестиугольник в природе, технике и культуре

• Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.
• Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
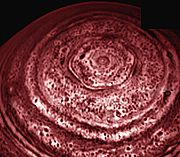
• Гигантский гексагон — атмосферное явление на Сатурне.
• Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
• Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
• Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
• Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.

Слева направо: Пчелиные соты; Графен — одна из аллотропных модификаций углерода; Гигантский гексагон.

Примечания

1. ↑ А. М. Райгородский Проблема Борсука. — М.: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9

Смотрите также

• Шестиугольник
• Упаковка кругов на плоскости

Ссылки

• Шестиугольный мир (ЖЖ-сообщество)