- Пятиугольник
-
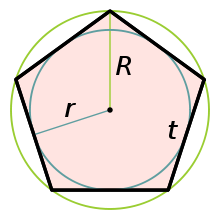 Правильный пятиугольник (пентагон)
Правильный пятиугольник (пентагон)
Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.
Сумма внутренних углов выпуклого пятиугольника равна 540°.
Если провести в пентагоне диагонали, то он разобьётся на[1]:
- меньший пентагон (образуеся точками пересечения диагоналей) — в центре
- Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию равным золотой пропорции):
- 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
- 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании
При соединении двух первых и двух вторых треугольников их основаниями, то получится два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (был назван плитками Пенроуза).
См. также
Примечания

Многоугольники По числу вершин 1-10 Одноугольник • Двуугольник • Треугольник • Четырёхугольник (Дельтоид) • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник 11-20 Одиннадцатиугольник (англ.) • Двенадцатиугольник Правильные Выпуклые Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • ... • 17-угольник • ... • 257-угольник • ... • 65537-угольник Звёздчатая форма Звезды (Пентаграмма • Гексаграмма • Октаграмма) Выпуклые Четырёхугольники: Параллелограмм • Прямоугольник • Ромб • Трапеция
ПланигонСм. также Теория и практика: Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника Категория:- Многоугольники
Wikimedia Foundation. 2010.


