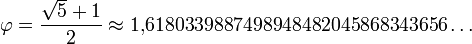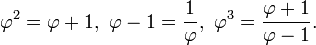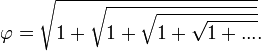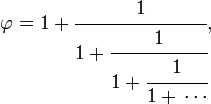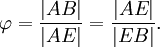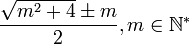Золотая пропорция

Вырезав квадрат со стороной а из прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же свойством

Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление, число Фидия) — деление непрерывной величины на части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Например, точка B делит отрезок AC так, что большая его часть AB относится к меньшей BC так, как весь отрезок AC относится к AB (то есть | AB | / | BC | = | AC | / | AB | ).

Эту пропорцию принято обозначать греческой буквой ϕ (встречается также обозначение τ). Она равна:

$\varphi = \frac{ \sqrt{5}+1}{2} \approx 1{,}6180339887498948482045868343656\dots$

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён Мартином Омом в 1835 году.

Математические свойства

Золотое сечение в пятиконечной звезде

• $\varphi$ — иррациональное алгебраическое число, положительное решение любого из следующих уравнений

  $\varphi^2 = \varphi + 1,\ \varphi - 1 = \frac{1}{\varphi}, \ \varphi ^ 3 = \frac{\varphi + 1}{\varphi - 1}.$

Вот ещё похожее представление:

$\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + ...}}}}.$

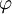• $\varphi\;$ представляется цепной дробью

  $\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1+\,\cdots}}},$

для которой подходящими дробями являются отношения последовательных чисел Фибоначчи 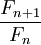$\frac{F_{n+1}}{F_n}$. Таким образом, $\varphi = \lim_{n\to\infty} \frac{F_{n+1}}{F_n}$.

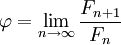• В правильной пятиконечной звезде каждый сегмент делится пересекающим его сегментом в золотом сечении (то есть отношение синего отрезка к зелёному, также как красного к синему, также как зелёного к фиолетовому, равны $\varphi\;$).

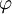Построение золотого сечения

• Геометрическое построение. Золотое сечение отрезка AB можно построить следующим образом: в точке B восстанавливается перпендикуляр к AB, откладывают на нём отрезок BC, равный половине AB, на отрезке AC откладывают отрезок AD, равный AC − CB, и наконец, на отрезке AB откладывают отрезок AE, равный AD. Тогда

  $\varphi=\frac{|AB|}{|AE|}=\frac{|AE|}{|EB|}.$

Золотое сечение и гармония

Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.

Архитектор Ле Корбюзье «нашёл», что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого сечения. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.

Ко всем этим утверждениям следует относиться с осторожностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения. Есть основание считать, что значимость золотого сечения в искусстве, архитектуре и в природе преувеличена и основывается на ошибочных расчётах. ^[1]

При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2 : 3), размеры кино- и телевизионных экранов — например, 3:4 или 9:16) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми».

"Золотое сечение" в искусстве

Золотое сечение и зрительные центры

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения».

Известно, что Сергей Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

Другим примером использования правила «Золотого сечения» в киноискусстве — расположение основных компонентов кадра в особых точках — «зрительных центрах». Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.

Следует заметить что в вышеописанных примерах фигурировало приблизительное значение "золотого сечения": легко убедиться что ни 3/2 ни 5/3 не равно значению золотого сечения.

Российский зодчий Жолтовский также использовал золотое сечение^[2].

Вариации и обобщения

• Формула «золотых гармоний», дающая пары чисел, удовлетворяющие вышеупомянутой пропорции:

  $\frac{\sqrt{m^2+4} \pm m}{2}, m\in\mathbb{N}^*$

В случае с числом $\varphi$ параметр m = 1.

См. также

• Пифагорейский пентакл
• Логарифмическая спираль
• Фибоначчиева система счисления
• Правило третей
• Метод золотого сечения

Источники

1. ↑ Радзюкевич А.В. Красивая сказка о «золотом сечении»
2. ↑ Золотой запас зодчества

Ссылки

• В. С. Белянин, "Владел ли Платон кодом золотой пропорции? Анализ мифа"
• А. Д. Бердукидзе, Золотое сечение Квант № 8, 1973.
• О. Н. Калюжный, Асимметричная рефлексия, Золотая Пропорция и алгоритм «Вальс»
• В. Лаврус, Золотое сечение
• Золотое сечение, как корень квадратного уравнения
• А. В. Радзюкевич Красивая сказка о золотом сечени
• А. В. Радзюкевич Знал ли Леонардо да Винчи «код да Винчи»?
• А. И. Щетников Золотое сечение в «древней» и в «новой» эстетике.
• Музей Гармонии и Золотого Сечения
• Институт Золотого Сечения
• Применение Золотого сечения в Web
• PyramidG программа для рассчета параметров пирамид золотого сечения