Формула Леви — Хинчина для устойчивого распределения

Усто́йчивое распределе́ние в теории вероятностей - это такое распределение, которое может быть получено как предел по распределению сумм независимых случайных величин.

Определение

Распределение 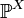$\mathbb{P}^X$ cлучайной величины X называется устойчивым, если для любого 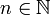$n\in \mathbb{N}$ существуют такие константы $a_n,b_n \in \mathbb{R}$, что распределение случайной величины a_nX + b_n совпадает с распределением суммы:

$a_n X + b_n =^{\!\!\!\!\! \mathcal{D}} \sum\limits_{i=1}^n Y_{n,i}$,

где равенство понимается в смысле равенства распределений, а случайные величины Y_n,i распределены как X, то есть $X=Y_{n,i} \sim \mathbb{P}^X,\; i=,\ldots,n$.

Замечания

• Если F_X - функция устойчивого распределения, то $\forall n \in \mathbb{N},\; \exists a_n,b_n \in \mathbb{R}$, такие что

$F_X\left(\frac{x-b_n}{a_n}\right) = F_X * \cdots * F(x),\quad \forall x \in \mathbb{R}$,

где * обозначает свёртку.

• Если φ_X - характеристическая функция устойчивого распределения, то $\forall n \in \mathbb{N},\; \exists a_n,b_n \in \mathbb{R}$, такие что

$\phi_X^n(t) = \phi_X(a_n t) \, e^{ib_n t}$.

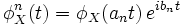Свойства устойчивых распределений

• Случайная величина имеет устойчивое распределение тогда и только тогда, когда она является пределом по распределению линейных комбинаций сумм независимых одинаково распределённых случайных величин. Более точно, случайная величина X может быть пределом по распределению случайных величин вида $\frac{S_n - b_n}{a_n}$, где

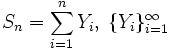$S_n = \sum\limits_{i=1}^n Y_i,\; \{Y_i\}_{i=1}^{\infty}$ - независимые одинаково распределённые случайные величины,

тогда и только тогда, когда распределение X устойчиво.

• (Представление Леви — Хинчина) Логарифм характеристической функции случайной величины с устойчивым распределением имеет вид:

$\ln \phi(t) = \left\{ \begin{matrix} it \beta - d |t|^{\alpha} \left(1 + i\theta \frac{t}{|t|} G(t,\alpha)\right), & t \not= 0 \\ 1, & t = 0. \end{matrix} \right.,$

где $0 < \alpha \le 2,\; \beta \in \mathbb{R},\; d \ge 0,\; |\theta| \le 1,$ и

$G(t,\alpha) = \left\{ \begin{matrix} \mathrm{tg} \frac{\pi}{2} \alpha, & \alpha \not= 1 \\ \frac{2}{\pi} \ln |t|, & \alpha = 1 \end{matrix} \right..$

См. также

• Бесконечно делимое распределение.

Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править