- Площадь
-
Площадь 
Размерность L²
Единицы измерения СИ СГС Примечания Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Содержание
Свойства
- Площадь единичного квадрата равна 1.
- Площадь аддитивна.
- Площадь неотрицательна.
- Площади конгруэнтных фигур равны.
Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими[2].
Общий метод определения площади
Площадь плоской фигуры
Декартовы координаты
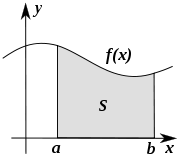
Площадь, заключённая между графиком непрерывной функции на интервале
![[a, b]](2c3d331bc98b44e71cb2aae9edadca7e.png) и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:Площадь, заключённая между графиками двух непрерывных функций
 на интервале
на интервале ![[a, b]](2c3d331bc98b44e71cb2aae9edadca7e.png) находится как разность определённых интегралов от этих функций:
находится как разность определённых интегралов от этих функций:
Полярные координаты
В полярных координатах: площадь, ограниченная графиком функции
 и лучами
и лучами  вычисляется по формуле:
вычисляется по формуле: .
.
Площадь поверхности
Площадь искривлённой поверхности A, заданной вектор-функцией
 , даётся двойным интегралом:
, даётся двойным интегралом:То же в координатах:
Здесь
 .
.Единицы измерения площади
Метрические единицы
- Квадратный километр, 1 км² = 1 000 000 м²
- Гектар, 1 га = 10 000 м²
- Ар (сотка), 1 а = 100 м²
- Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м².
Русские устаревшие
- Квадратная верста = 1,13806 км²
- Десятина = 10925,4 м²
- Копна = 0,1 десятины — сенные покосы меряли копнами
- Квадратная сажень = 4,55224 м²
Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.
Античные
Формулы вычисления площадей простейших фигур
Планиметрические фигуры
Фигура Формула Переменные Квадрат 
 — длина стороны квадрата.
— длина стороны квадрата.Правильный треугольник 
 — длина стороны треугольника.
— длина стороны треугольника.Правильный шестиугольник 
 — длина стороны шестиугольника.
— длина стороны шестиугольника.Правильный восьмиугольник 
 — длина стороны восьмиугольника.
— длина стороны восьмиугольника.Правильный многоугольник 
 — периметр, а
— периметр, а  — количество сторон.
— количество сторон.Прямоугольный треугольник 
 и
и  — катеты треугольника.
— катеты треугольника.Произвольный треугольник 
 — сторона треугольника,
— сторона треугольника,  — высота, проведенная к этой стороне.
— высота, проведенная к этой стороне.
 ,
,  — любые две стороны,
— любые две стороны,  — угол между ними.
— угол между ними. (формула Герона)
(формула Герона) ,
,  ,
,  — стороны треугольника,
— стороны треугольника,  — полупериметр
— полупериметр  .
.
в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный. Прямоугольник 
 и
и  — длины сторон прямоугольника (его длина и ширина).
— длины сторон прямоугольника (его длина и ширина).Параллелограмм 
 и
и  — длина стороны и опущенной на неё высоты соответственно.
— длина стороны и опущенной на неё высоты соответственно.
 и
и  — соседние стороны параллелограмма,
— соседние стороны параллелограмма,  — угол между ними.
— угол между ними.Ромб 
 и
и  — длины диагоналей ромба.
— длины диагоналей ромба.Эллипс 
 и
и  — длины малой и большой полуосей.
— длины малой и большой полуосей.Трапеция 
 та
та  — параллельные стороны, и
— параллельные стороны, и  — расстояние между ними (высота трапеции).
— расстояние между ними (высота трапеции).Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур
Фигура Формула Переменные Круг  или
или 
 — радиус, а
— радиус, а  — диаметр круга.
— диаметр круга.Сектор круга 
 — радиус круга,
— радиус круга,  — центральный угол сектора (в радианах).
— центральный угол сектора (в радианах).Сегмент 
 — радиус круга,
— радиус круга,  — центральный угол сегмента (в радианах).
— центральный угол сегмента (в радианах).Треугольник, вписанный в окружность 
 ,
,  ,
,  — стороны треугольника,
— стороны треугольника,  — радиус описанной окружности.
— радиус описанной окружности.Произвольный многоугольник, описанный вокруг окружности 
 — радиус окружности, вписанной в многоугольник, и
— радиус окружности, вписанной в многоугольник, и  — периметр многоугольника.
— периметр многоугольника.Формулы для вычисления площади поверхности тел в пространстве
Тело Формула Переменные Полная площадь поверхности цилиндра 
 и
и  — радиус и высота соответственно.
— радиус и высота соответственно.Площадь боковой поверхности цилиндра 
 и
и  — радиус и высота соответственно.
— радиус и высота соответственно.Полная площадь конуса 
 и
и  — радиус и высота боковой поверхности соответственно.
— радиус и высота боковой поверхности соответственно.Площадь боковой поверхности конуса 
 и
и  — радиус и образующая боковой поверхности соответственно.
— радиус и образующая боковой поверхности соответственно.Площадь поверхности сферы (шара)  или
или 
 и
и  радиус и диаметр, соответственно.
радиус и диаметр, соответственно.См. также
- Площадь фигуры — математические аспекты понятия.
- Длина кривой
- Квадратура (математика)
- Объём
- Поверхность
Литература
- Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
Ссылки
- Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
- Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.
Примечания
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.
Категории:- Физические величины по алфавиту
- Площадь
Wikimedia Foundation. 2010.