- Алгебра (теория множеств)
-
Алгебра (теория множеств)
Алгебра множеств в теории множеств — это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы).
Содержание
Определение
Семейство
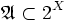 подмножеств множества X называется алгеброй, если оно удовлетворяет следующим свойствам:
подмножеств множества X называется алгеброй, если оно удовлетворяет следующим свойствам: содержит пустое множество
содержит пустое множество 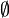 .
.- Если
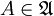 , то и его дополнение
, то и его дополнение 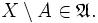
- Объединение двух множеств
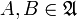 также принадлежит
также принадлежит 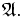
Замечания
- В силу свойств операций над множествами, алгебра множеств также замкнута относительно пересечения и симметрической разности.
- Алгебра множеств — это частный случай алгебры с единицей, где операцией «умножения» является пересечение множеств, а операцией «сложения» является симметрическая разность.
- Если исходное множество X является пространством элементарных событий, то алгебра
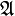 называется алгеброй событий — ключевое понятие теории вероятностей и связанных с ней математических дисциплин, имеющее уникальную интерпретацию и играющее самостоятельную роль в математике.
называется алгеброй событий — ключевое понятие теории вероятностей и связанных с ней математических дисциплин, имеющее уникальную интерпретацию и играющее самостоятельную роль в математике.
Алгебра событий
Алгебра событий (в теории вероятностей) — алгебра подмножеств пространства элементарных событий
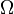 , элементами которого служат элементарные события.
, элементами которого служат элементарные события.Как и положено алгебре множеств алгебра событий содержит невозможное событие (пустое множество) и замкнута относительно теоретико-множественных операций, производимых в конечном числе. Достаточно потребовать, чтобы алгебра событий была замкнута относительно двух операций, например, пересечения и дополнения, из чего сразу последует её замкнутость относительно любых других теоретико-множественных операций. Алгебра событий, замкнутая относительно счётного числа теоретико-множественных операций, называется сигма-алгеброй событий.
В теории вероятностей встречаются следующие алгебры и сигма-алгебры событий:
- алгебра конечных подмножеств
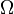 ;
; - сигма-алгебра счётных подмножеств
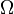 ;
; - алгебра подмножеств
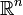 , образованная конечными объединениями интервалов;
, образованная конечными объединениями интервалов; - сигма-алгебра борелевских подмножеств топологического пространства
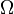 , то есть наименьшая сигма-алгебра, содержащая все открытые подмножества
, то есть наименьшая сигма-алгебра, содержащая все открытые подмножества 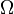 ;
; - алгебра цилиндров в пространстве функций и сигма-алгебра, ими порожденная.
Алгебры и сигма-алгебры событий — это области определения вероятности
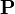 . Если
. Если 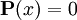 , то событие
, то событие 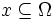 называется невозможным событием; если
называется невозможным событием; если 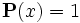 , то событие
, то событие 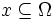 называется достоверным событием;
называется достоверным событием;Любая сигма-аддитивная вероятность на алгебре событий однозначно продолжается до сигма-аддитивной вероятности, определенной на сигма-алгебре событий, порожденной данной алгеброй событий.
См. также
- Сигма-алгебра
- Кольцо
- Полукольцо
- Аксиоматика Колмогорова
- Элементарное событие
- Событие (теория вероятностей)
- Вероятностное пространство
Литература
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.
Wikimedia Foundation. 2010.
