- Программируемые алгоритмы
-
Нижеследующее — это список алгоритмов. Также смотрите список структур данных, список основных разделов теории алгоритмов и список терминов, относящихся к алгоритмам и структурам данных.
Если Вы планируете добавить какой-либо алгоритм в этот список, убедитесь, пожалуйста, что его здесь ещё нет (возможно, алгоритм упоминается под каким-либо альтернативным названием). Внимательно посмотрите, к какой именно категории относится данный алгоритм. В случае, когда из названия не ясно, что именно делает алгоритм, напишите, пожалуйста, краткое описание.
Если Вы планируете написать статью про один из алгоритмов, упомянутых в этом списке, пожалуйста, прочитайте сначала руководство «Википедия:Алгоритмы в Википедии (англ.)» или посмотрите несколько уже написанных статей, посвящённых алгоритмам.
Комбинаторные алгоритмы
Общие комбинаторные алгоритмы
- Алгоритм Флойда для нахождения циклов — находит цикл в итерациях
- Генераторы псевдослучайных чисел:
- Алгоритм Робинсона — Шенстеда (англ.) — генерация перестановок из пар таблиц Юнга
Алгоритмы на графах
- Алгоритм Беллмана — Форда — вычисляет кратчайший путь во взвешенном графе (где некоторые веса рёбер могут быть отрицательны)
- Алгоритм Борувки — находит минимальное остовное дерево в графе
- Алгоритм Брона — Кербоша — нахождение наибольших максимальных независимых по включению множеств вершин графа.
- Алгоритм Флойда — Уоршелла — вычисляет все кратчайшие пути во взвешенном графе
- Алгоритм Дейкстры — вычисляет кратчайший путь в графе с неотрицательными весами рёбер
- Алгоритм Джонсона — вычисляет все кратчайшие пути во взвешенном графе
- Алгоритм Краскала — находит остовный лес минимального веса в графе
- Алгоритм основанный на источнике (англ.) — алгоритм для рисования графа
- Алгоритм Прима — находит остовное дерево минимального веса в связном графе
- Алгоритм Кристофидеса — эвристический приближенный алгоритм для решения метрической задачи коммивояжера на графе.
- Метод ближайшего соседа
- Неблокирующий минимальный охватывающий переключатель например, для телефонной связи
- Построение транзитивного замыкания графа (установление факта достижимости вершин)
Алгоритмы нахождения максимального потока
- Алгоритм Форда — Фалкерсона
- Алгоритм Эдмондса — Карпа, кратчайших увеличивающихся цепей (англ.)
- Алгоритм Эдмондса — Карпа, локально-максимального увеличения
- Алгоритм Диница
- Алгоритм Карзанова
- Алгоритм Малхотри — Кумара — Махешвари
- Алгоритм Галила — Наамада
- Алгоритм Слейтора — Тарьяна
- Алгоритм Голдберга — Тарьяна
- Алгоритм CHM
- Алгоритм Кинга
- Алгоритм Голдберга — Рао
Алгоритмы нахождения максимального паросочетания
- Алгоритм Хопкрофта — Карпа
- Алгоритм Форда — Фалкерсона
- Алгоритм Куна
- Алгоритм Габоу
Алгоритмы поиска
- Алгоритм поиска A* — особый случай поиска по первому наилучшему совпадению; используется эвристика, увеличивающая скорость работы алгоритма
- Алгоритм выбора (англ.) — модификация алгоритма линейного поиска; находит k-тый по величине элемент в списке;
- Дерево двоичного поиска (англ.) — использует бинарное дерево для хранения элементов;
- Двоичный поиск — находит элемент в отсортированном списке
- Интерполирующий поиск (Предсказывающий поиск, Поиск по словарю)
- Линейный поиск — находит элемент в неотсортированном списке
- Локальный поиск (оптимизация)
- Метод штрафов (англ.)
- Поиск в глубину — проходит граф ветка за веткой
- Поиск в ширину — проходит граф уровень за уровнем
- Поиск по первому наилучшему совпадению (англ.) (англ. Best-first search) — проходит граф в порядке важности, используя очередь приоритетов
- Троичный поиск — находит максимум или минимум функции
- Поиск в хеш-таблице
- Алгоритм Ли (волновой алгоритм) — поиск пути на карте.
Алгоритмы на строках
Алгоритмы поиска строки
- Алгоритм Кнута — Морриса — Пратта
- Алгоритм Рабина — Карпа поиска строки
- Алгоритм Бойера — Мура поиска строки
- Алгоритм Ахо — Корасик
- Алгоритм Битапа (англ.) (также известен как shift-or, shift-and или алгоритм Баеса-Ятеса[1] — Гоннета)
- Задача поиска наибольшей общей подпоследовательности
- Задача поиска наибольшей увеличивающейся подпоследовательности
- Задача поиска наикратчайшей общей надпоследовательности (англ.)
- Задача поиска наибольшей общей подстроки
- Задача поиска количества подпалиндромов
Примерное соответствие
- Расстояние Левенштейна
- Расстояние Хэмминга
- Расстояние Дамерау — Левенштейна
- Алгоритм Нидлмана — Вунша (англ.)
- Алгоритм Смита — Вотермана (англ.)
- Metaphone
Деревья для строковых последовательностей
- Суффиксное дерево
- Алгоритм Мак-Крейта
- Алгоритм Укконена
- Алгоритм Вайнера
- Алгоритм Фрача
- Суффиксные массивы
Алгоритмы сортировки
- Bogosort (англ.)
- Наивная сортировка — генерация всех n! возможных перестановок и проверка на отсортированность
- Блинная сортировка (англ.)
- Блочная сортировка (также известен как корзинная сортировка), ср. с поразрядной
- Быстрая сортировка — с разбиением исходного набора данных на две половины так, что любой элемент первой половины упорядочен относительно любого элемента второй половины; затем алгоритм применяется рекурсивно к каждой половине
- Глупая сортировка, найти отличия от Bogosort
- Гномья сортировка (англ.)
- Пирамидальная сортировка (Сортировка кучей) — превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
- Плавная сортировка (англ.)
- Поразрядная сортировка — сортирует строки буква за буквой (ср. с блочной)
- Сортировка Бентли — Седжвика (англ. BeSe sort) — модификация быстрой сортировки для составных ключей, заключающаяся в делении не пополам, а на три части — в третью попадают одинаковые (по текущему символу) ключи
- Сортировка бинарным деревом
- Сортировка методом вставок — определяем, где текущий элемент должен находится в отсортированном списке, и вставляем его туда
- Сортировка методом выбора — наименьшего или наибольшего элемента и помещения его в начало или конец отсортированного списка
- Сортировка методом Шелла — попытка улучшить сортировку вставками
- Сортировка перемешиванием (Сортировка коктейлем)
- Сортировка подсчётом — используется диапазон входных данных, подсчитывается число одинаковых элементов (3 варианта)
- Сортировка пузырьком
- Сортировка расчёской (англ.)
- Сортировка слиянием — сортируем первую и вторую половину списка отдельно, а затем — сливаем отсортированные списки
- Топологическая сортировка
- Хитрая сортировка — извлекает из исходной последовательности отсортированные подпоследовательности, производя их слияние с уже извлечёнными данными
- Цифровая сортировка (Сортировка по отделениям)
Алгоритмы слияния
- Простой алгоритм слияния (англ. Simple Merge algorithm )
- k-мерный алгоритм слияния (англ. k-way Merge algorithm )
Алгоритмы сжатия данных
Алгоритмы сжатия без потерь
- Преобразование Барроуза — Уилера (также известен как англ. BWT) — предварительная обработка данных для улучшения сжатия без потерь
- Преобразование Шиндлера (англ. ST) — модификация преобразования Барроуза — Уилера
- Алгоритм DEFLATE (англ.)
- Дельта-кодирование — эффективно для сжатия данных, в которых последовательности часто повторяются
- Инкрементное кодирование — дельта-кодирование применяемое к последовательности строк
- Семейство алгоритмов словарного сжатия :
- LZ78 — родоначальник семейства LZ78 алгоритмов
- Алгоритм Лемпеля — Зива — Велча (также известен как англ. LZW) — сжатие без потерь
- LZW-PM
- LZMW
- Алгоритм Лемпеля — Зива — Велча (также известен как англ. LZW) — сжатие без потерь
- англ. Lempel-Ziv-Markov chain-Algorithm
- Алгоритм сжатия PPM
- Кодирование длин серий (Групповое кодирование, также известен как англ. RLE) — последовательная серия одинаковых элементов заменяется на два символа: элемент и число его повторений
- Алгоритм SEQUITUR (англ.) — сжатие без потерь, автоматическое адаптивное построение контекстно-свободной грамматики для обрабатываемых данных
- Вейвлет-кодирование на основе вложенных нуль-деревьев (англ.) (EZW-кодирование)
- Энтропийное кодирование — схема кодирования, которая присваивает коды символам таким образом, чтобы соотнести длину кодов с вероятностью появления символов
- Алгоритм Шеннона — Фано — самый простой алгоритм кодирования
- Алгоритм Хаффмана — алгоритм построения кода при помощи кодовых деревьев
- Адаптивное кодирование Хаффмана (англ.) — техника адаптивного кодирования, основывающаяся на коде Хаффмана
- Усечённое двоичное кодирование (англ.) — используется для однородного вероятностного распределения с конечным алфавитом
- Арифметическое кодирование — развитие энтропийного кодирования
- Адаптивное арифметическое кодирование — техника адаптивного кодирования, основывающаяся на арифметическом кодировании
- Кодирование расстояний (англ.) — метод сжатия данных, который близок по эффективности к арифметическому кодированию
- Энтропийное кодирование с известными характеристиками
- Унарное кодирование — код, который представляет число n в виде n единиц с замыкающим нулём
- дельта|гамма|омега-кодирование Элиаса (англ. Elias coding) — универсальный код, кодирующий положительные целые числа
- Кодирование Фибоначчи — универсальный код, который кодирует положительные целые числа в двоичные кодовые слова
- Кодирование Голомба — форма энтропийного кодирования, которая оптимальна для алфавитов с геометрическим распределением
- Кодирование Райса (англ.) — форма энтропийного кодирования, которая оптимальна для алфавитов с геометрическим распределением
Алгоритмы сжатия с потерями
- Линейное предсказывающее кодирование (англ.) — сжатие с потерями, представляющее спектральную огибающую цифрового сигнала речи в сжатом виде
- А-закон — стандартный алгоритм компандирования. Применяется в РФ.
- Мю-закон — стандартный алгоритм компандирования
- Фрактальное сжатие — метод, использующий фракталы для сжатия изображений
- Трансформирующее кодирование (англ.) — тип сжатия данных для «естественных» данных, таких как аудио-сигналы или фотографические изображения
- Векторная квантизация (англ.) — техника, часто используемая в сжатии данных с потерями
- Вейвлетное сжатие — тип компрессии данных хорошо подходящий для сжатия изображений (иногда также используется для сжатия видео и аудио)
Вычислительная геометрия
- Алгоритм расстояния Гильберта — Джонсона — Кеерти (англ.) — определение наименьшего расстояния между двумя выпуклыми фигурами
- Поиск пары ближайших точек (англ.) — трудоёмкость O(nlogn).
- Поиск диаметра множества точек
- Алгоритм Цируса — Бека — отсечение линий.
- Алгоритм Сазерленда — Ходжмана — отсечение многоугольника.
- Построения контура прямоугольников (стороны параллельны осям координат).
- Нахождение ядра многоугольника
- Регуляризация многоугольника — декомпозиция многоугольника на монотонные части.
Построение выпуклой оболочки набора точек
- Построение ВП через треугольники — трудоёмкость O(n4).
- Построение ВП перебором рёбер на принадлежность — трудоёмкость O(n3).
- Алгоритм сканирования Грэхема — трудоёмкость O(nlogn).
- Алгоритм Экла — Туссена — трудоёмкость O(nlogn). Улучшение алгоритма Грэхема.
- Алгоритм Эндрю — трудоёмкость O(nlogn). Улучшение алгоритма Грэхема.
- Алгоритм быстрой оболочки — трудоёмкость O(n2), в среднем — O(nlogn).
- Алгоритм Киркпатрика — построение выпуклой оболочки набора точек на плоскости методом «разделяй и властвуй» через мосты. Трудоёмкость O(nlogn).
- Построение методом «разделяй и властвуй» через построение касательных — трудоёмкость O(nlogn).
- Алгоритм заворачивания подарков (Джарвиса) — трудоёмкость O(nh), h — количество точек в выпуклой оболочке.
- Алгоритм Киркпатрика — Зейделя (англ.) — трудоёмкость O(nlogh), h — количество точек в выпуклой оболочке.
- Алгоритм Чана — трудоёмкость O(nlogh), h — количество точек в выпуклой оболочке.
- Инкрементальный алгоритм (fast online hull) — через построение касательных O(n2), с помощью сбалансированного дерева — O(nlogn).
- Приближённая выпуклая оболочка снизу (lower approximate hull) — методом полос. Трудоёмкость O(nk), где k — количество полос.
- Приближённая выпуклая оболочка сверху (upper approximate hull) — методом полос. Трудоёмкость O(nk), где k — количество полос.
- Алгоритм Ли (выпуклые оболочки) — построение выпуклой оболочки простого многоугольника через отрезание карманов. Трудоёмкость O(n).
Триангуляция
- Триангуляция через поиск диагоналей — ищется диагональ, многоугольник делится на два и далее рекурсивно. Трудоёмкость O(n4).
- Триангуляция через отрезание ушей — ищется образующая треугольник диагональ, соседние с треугольником вершины — следующие претенденты на отрезание. Трудоёмкость O(n2).
- Триангуляция монотонного простого многоугольника — трудоёмкость O(n).
- Жадная триангуляция — трудоёмкость O(n2logn).
- Оптимальная триангуляция — NP-полная задача. Суммарная длина всех рёбер минимальна среди всех триангуляций данного множества.
Триангуляция Делоне
- Итеративные алгоритмы построения триангуляции Делоне — трудоёмкость O(n2).
- Алгоритмы построения триангуляциии Делоне слиянием — трудоёмкость O(n2) и O(nlogn).
- Алгоритмы прямого построения триангуляциии Делоне — трудоёмкость O(n2).
- Двухпроходные алгоритмы построения триангуляциии Делоне — трудоёмкость O(n2) и O(nlogn).
- Триангуляциии Делоне с ограничениями — трудоёмкость O(n2).
Диаграмма Вороного
- Простой алгоритм построения диаграммы Вороного — трудоёмкость O(n2logn).
- Алгоритм построения диаграммы Вороного через заметающую прямую — трудоёмкость O(nlogn).
- Рекурсивный алгоритм построения диаграммы Вороного — трудоёмкость O(nlogn).
Локализация точки (англ.)
- Локализация точки для выпуклого многоугольника — время запроса O(logn).
- Локализация точки в звездном многоугольнике — время запроса O(logn).
- Алгоритм точки в многоугольнике — проверка принадлежности данной точки простому многоугольнику O(n).
- Метод луча — принадлежность точки простому многоугольнику O(n).
- Метод углов — принадлежность точки выпуклому многоугольнику. Трудоёмкость O(n).
- Метод полос — простой многоугольник. Время запроса O(logn), память O(n2).
- Метод детализации триангуляции Киркпатрика — простой многоугольник. Время запроса O(logn), память O(n).
- Трапецоидальная карта — простой многоугольник. Рандомизированный алгоритм, время запроса O(logn), память O(n).
- Метод цепей — простой многоугольник. Время запроса O(log2n), память O(n).
Пересечения
- Пересечение отрезков (алгоритм Бентли — Оттманна) — поиск всех точек пересечения отрезков на плоскости O((n + k)logn), k — количество точек пересечения.
- Алгоритм Чазелла — Эдельсбруннера — пересечение отрезков за O(k + nlogn).
- Определение наличия пересекающихся отрезков (англ.) (алгоритм Шеймоса — Гоя) — трудоёмкость O(nlogn).
- Алгоритм Сазерленда — Коэна — для выпуклых многоугольников. Трудоёмкость O(n1n2).
- Пересечения выпуклых многоугольников — трудоёмкость O(n1 + n2).
- Алгоритм Шеймоса — Хоуи — для выпуклых многоугольников методом полос. Трудоёмкость O(n1 + n2).
- Пересечения выпуклых многоугольников с заметающей прямой — трудоёмкость O(n1 + n2).
- Пересечение звёздных многоугольников — трудоёмкость O(n1n2).
- Пересечение полуплоскостей — трудоёмкость O(nlogn).
Вращающиеся калиперы (англ.)
- Поиск диаметра множества точек через вращающиеся калиперы
- Поиск минимального по площади описанного прямоугольника для множества точек (англ.)
- Поиск минимального по периметру описанного прямоугольника для множества точек (англ.)
- Определение ширины многоугольника
- Построение суммы Минковского двух выпуклых многоугольников
- Поиск максимального расстояния между двумя множествами точек
- Поиск минимального расстояния между двумя выпуклыми многоугольниками
- Построение мостов для двух выпуклых многоугольников
- Построение критических опорных прямых для выпуклых многоугольников
Компьютерная графика
- Алгоритм Брезенхэма — растеризует отрезок линии с заданными координатами начала и конца
- Алгоритм рисования прямой (англ.) — алгоритм для аппроксимации отрезка на дискретной графической поверхности
- Алгоритм DDA-линии — чертит точки двухмерного массива в форме прямой линии между двумя заданными точками (использует вычисления с плавающей точкой)
- Алгоритм заливки области (англ.) — заполняет соединённый регион многомерного массива указанным значением
- Алгоритм Ву — алгоритм для сглаживания прямой
- Алгоритм художника (англ.) — определяет видимые части трёхмерной сцены
- Алгоритм лучевой трассировки (англ.) — рендеринг реалистичных изображений
- Затенение по Фонгу — модель освещения и метод интерполяции в трёхмерной компьютерной графике
- Затенение по Гуро — алгоритм моделирования различных эффектов света и цвета на поверхности объекта в трёхмерной компьютерной графике
- Изображение сканирующей линией (англ.) (англ. Scanline rendering) — конструирует образ с помощью перемещения воображаемой линии над образом
- Алгоритмы глобального освещения (англ.) — рассматривает прямое освещение и отражение от других объектов
- Алгоритмы интерполяции — конструирование новых точек данных, таких как в цифровом увеличителе
- Интерполяция сплайнами (англ.) — уменьшение ошибки с помощью феномена Рунге (англ.)
Компьютерное зрение
- Epitome (англ.) — представление образа или видео при помощи меньшего образа или видео
Криптографические алгоритмы
- См. также Разделы в криптографии для аналитического глоссария
- Шифрование с симметричным (скрытым) ключом:
- ГОСТ 28147-89
- AES (англ. Advanced Encryption Standard) — победитель соревнования NIST, также известен как Rijndael
- Blowfish
- англ. Data Encryption Standard) — иногда, алгоритм DEA (англ. Data Encryption Algorithm), победитель соревнования NBS, заменён на AES для большинства применений
- RC2
- англ. International Data Encryption Algorithm)
- Асимметричное шифрование (с публичным ключом)
- Алгоритмы цифровой подписи:
- ГОСТ Р 34.10-94 — устаревший российский стандарт цифровой подписи, модификация схемы Эль-Гамаля
- ГОСТ Р 34.10-2001 — российский стандарт цифровой подписи, основанный на эллиптических кривых
- англ. Digital Signature Algorithm) — базируется на схеме Эль-Гамаля
- англ. Elliptic Curve Digital Signature Algorithm) — перенос DSA на эллиптические кривые
- Алгоритмы разделения секрета
- Рюкзак — на данный момент доказана нестойкость схемы
- Схема Шамира
- Схема Blakey
- Алгоритмы подбрасывания монеты по телефону
- Криптографические функции дайджестов сообщений:
- ГОСТ Р 34.11-94
- RFC 1321) — существует метод генерации коллизий
- SHA-1
-
- Криптостойкие генераторы псевдослучайных чисел
- Алгоритм Блюма — Блюма — Шуба — базируется на сложности факторизации
- Алгоритм Ярроу (англ.)
- ГПСЧ Фортуна (англ.) — якобы улучшение алгоритма Ярроу
- Генерация случайных простых чисел
Цифровая обработка сигналов
- тригонометрических функций.
- Медианный фильтр для одномерного массива
- Дождевой алгоритм (англ.) — Уменьшает комплексную историю давлений в расчёте элементарных противодействий для использования в анализе усталости
- Osem — алгоритм для обработки медицинских изображений
- Алгоритм Гэртцеля (англ.) — Может быть использован для декодирования цифр тональных сигналов
- Развеяние Ричардсона — Люси (англ.) — алгоритм увеличения резкости образа
Разработка программного обеспечения
- Алгоритмы для восстановления и изоляции повреждённых семантик (англ.)
- Алгоритм сравнения Unicode (англ.)
- Алгоритм преобразования CHS (англ.) — Преобразование между системами адресации диска
- Алгоритм вычисления контрольной суммы (CRC или FCS) Циклическая избыточная сумма (Ciclic Redunancy Check), или контрольная последовательность кадра (Frame Check Sequence) — вычисление кода проверки.
- Чётность — Проверка четности количества единиц в двоичной записи числа. Позволяет обнаруживать ошибку в одном разряде.
- Алгоритм соединения (СУБД) — реализация операции соединения реляционной алгебры.
Алгоритмы распределённых систем
- Упорядочение Лампорта (англ.) — Частичное упорядочение событий в зависимости от того, что случилось раньше
- Алгоритм мгновенного снимка (англ.) — снимок процесса записывающий глобальное состояние системы
- Векторное упорядочение (англ.) — Полное упорядочение событий
- Алгоритм Марцулло (англ.) — распределённая синхронизация часов
- Алгоритм пересечений (англ.) — другой алгоритм синхронизации часов
Алгоритмы выделения и освобождения памяти
- Сборщик мусора Боема (англ.) — «скромный» сборщик мусора
- Дружеское выделение памяти (англ.) — алгоритм выделения памяти таким образом, чтобы фрагментация была наименьшей.
- Обобщённый сборщик мусора (англ.) — Быстрые сборщики мусора, которые разделяют память по возрасту
- Пометить и вымести (англ.)
- Подсчёт ссылок
Алгоритмы в операционных системах
- Алгоритм банкира (англ.) — Алгоритм, использующийся для избежания взаимных блокировок
- Алгоритм замены страницы (англ.) — выбор страницы-жертвы при условиях небольшого объёма памяти
- Алгоритм забияки (англ.) — выбор нового лидера среди множества компьютеров
Дисковые алгоритмы-планировщики
- Алгоритм лифта (англ.) — дисковый алгоритм планирования, который работает как лифт
- Первым ищется кратчайший (англ.) — дисковый алгоритм планирования для уменьшения времени поиска
Алгоритмы синхронизации процессов
- Алгоритм Петерсона
- Алгоритм пекарни Лампорта (англ.)
- Алгоритм Деккера (англ.)
- Планирование с постоянной скоростью (англ.)
- Первый заканчивает раньше (планирование) (англ.)
- Честное разделение (планирование) (англ.)
- Планирование по кругу (англ.)
- Многоуровневая отдача (планирование) (англ.) (англ. Multi level feedback queue)
- Кратчайшая работа следующей (планирование)
- Кратчайшее оставшееся время (планирование) (англ.)
- Наименьшее время бездействия (планирование) (англ.)
- Списковое планирование (англ.) (англ. List scheduling)
Генетические алгоритмы
- Выбор пропорционально пригодности (англ.) — также известен как выбор рулеточного колеса
Медицинские алгоритмы
- Медицинский алгоритм (англ.)
- Техасский проект медицинских алгоритмов (англ.)
Нейронные сети
- Метод обратного распространения ошибки
- Самоорганизующееся отображение (Карты Кохонена, SOM)
- Метод коррекции ошибки
- Метод коррекции с обратной передачей сигнала ошибки
Вычислительная алгебра
- Алгоритм Бухбергера (англ.) — находит базис Грёбнера
- Процесс Грама — Шмидта (англ.) — ортогонализация набора векторов
- Алгоритм пополнения Кнута — Бендикса (англ.)
- Алгоритм мультивариационного деления (англ.) — для многочленов в некоторых неопределённостях
- Алгоритмы умножения матриц
- Алгоритм Штрассена — быстрое умножение матриц
- Алгоритм Копперсмита — Винограда
- Умножение цепных матриц (англ.) (англ. Chain matrix multiplication)
- Алгоритмы вычисления дискретного преобразования Фурье
- Быстрое преобразование Фурье
- Алгоритм БПФ Кули — Туки (англ.)
- Алгоритм БПФ Рэдера (англ.)
- Алгоритм БПФ Блюштейна (англ.)
- Алгоритм БПФ Брууна (англ.)
- Алгоритм БПФ при помощи простых сомножителей (англ.)
- Алгоритм нахождения собственного значения матрицы (англ.)
- Преобразования Хаусхолдера (QR-разложение) — вычисление обратной матрицы, собственный векторов и собственных значений матрицы; используется также для решения систем линейных уравнений.
- Решение систем линейных уравнений
- Метод Гаусса (Гауссово исключение) — стандартный метод решения систем линейных уравнений
- Структурированное гауссово исключение — применяется, когда матрица системы является разреженной
- Метод Жордана — Гаусса — модификация метода Гаусса для матричного представления
- Преобразования Холеского — метод, эффективный для ленточных и разреженных матриц
- Метод Пранис — Праневича — решение систем линейных уравнений с параллельными вычислениями по компонентам
Теоретико-числовые алгоритмы
- Целочисленная арифметика (алгоритмы для работы с большими числами)
- Умножение столбиком больших чисел
- «Быстрый столбик»
- Умножение Карацубы — алгоритм быстрого умножения чисел
- Деление на одноразрядное число (DO)
- Деление больших чисел
- Быстрое возведение в степень — вычисляет степени чисел при помощи возведения в квадрат
- Алгоритмы модулярной арифметики
- Алгоритм Монтгомери — модулярное умножение и возведение в степень
- Алгоритм нахождения порядка элемента
- Алгоритм Тонелли — Шенкса — решение квадратичных сравнений
- Решение систем линейных сравнений
- С помощью китайской теоремы об остатках
- Алгоритм Гарнера
- Решение систем линейных уравнений над полем
- Алгоритм Ланцоша — эффективен над полем характеристики 2
- Алгоритм Видемана
- Дискретное логарифмирование:
- В простом конечном поле
- Алгоритм Шенкса (англ.) (алгоритм больших и маленьких шагов, англ. baby-step giant-step)
- Алгоритм Полига — Хеллмана — эффективен, если все делители p − 1 — небольшие
- ρ-метод Полларда дискретного логарифмирования
- Алгоритм Адлемана — первый субэкспоненциальный алгоритм дискретного логарифмирования
- Алгоритм COS (алгоритм Копперсмита — Одлыжко — Шреппеля) — достаточно эффективный субэкспоненциальный алгоритм
- Решето числового поля — наиболее эффективный на данный момент алгоритм дискретного логарифмирования
- В произвольном конечном поле
- Алгоритм исчисления индексов (англ.) (алгоритм index-calculus) — сведение дискретного логарифмирования в произвольном конечном поле к аналогичной задаче в простом поле
- Алгоритм Копперсмита — эффективный алгоритм дискретного логарифмирования в конечном поле характеристики 2
- В простом конечном поле
- Алгоритмы нахождения наибольшего общего делителя (НОД) двух чисел
- Алгоритм Евклида
- Расширенный алгоритм Евклида — также решает уравнение ax + by = c, где c = НОД
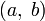 , НОД
, НОД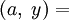 НОД
НОД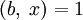
- Бинарный алгоритм нахождения НОД — эффективный способ вычисления НОД
- Расширенный бинарный алгоритм — модификация бинарного алгоритма нахождения НОД, аналогичная расширенному алгоритму Евклида
- Тесты простоты — проверка, является ли данное число простым
- Детерминированные тесты простоты
- Перебор делителей
- Решето Эратосфена
- Решето Аткина — оптимизированная версия решета Эратосфена
- Тест на основе малой теоремы Ферма
- Тест Миллера — модификация теста на основе малой теоремы Ферма; опирается на расширенную гипотезу Римана
- (N-1)–метод проверки простоты — тест на простоту при известном разложении на множители числа N − 1; также используется для построения больших простых чисел
- (N+1)–метод проверки простоты — тест на простоту при известном разложении на множители числа N + 1
- Алгоритм Конягина — Померанса — модификация (N − 1)-метода
- Алгоритм Ленстры — использует суммы Якоби и некоторые тесты, обобщающие малую теорему Ферма
- Тест Люка — Лемера для чисел Мерсенна
- Тест Пепина для чисел Ферма
- Тест простоты AKS (англ.) (тест Агравала, Кайала, Саксены) — полиномиальный детерминированный тест на простоту
- Вероятностные тесты простоты
- Тест Соловея — Штрассена — опирается на малую теорему Ферма и свойства символа Лежандра
- Тест Миллера — Рабина — эффективная модификация теста Соловея — Штрассена
- Детерминированные тесты простоты
- Факторизация — разложение числа на множители
- Алгоритмы с экспоненциальной сложностью
- Перебор делителей
- Метод факторизации Ферма (англ.)
- (p-1)-алгоритм Полларда (англ.)
- ρ-метод Полларда
- Алгоритм Шермана — Лемана
- Алгоритм Ленстры
- Алгоритмы с субэкспоненциальной сложностью
- Алгоритм Диксона (англ.)
- Квадратичное решето (англ.)
- Специальное решето числового поля (англ.) (англ. SNFS)
- Общее решето числового поля (англ.) (англ. GNFS)
- Алгоритм Ленстры (с помощью эллиптических кривых) (англ.) — вероятностный алгоритм факторизации с помощью эллиптических кривых
- Алгоритмы с экспоненциальной сложностью
- Алгоритм Шуфа — вычисление порядка группы точек эллиптической кривой
- Алгоритм Ленстры — Ленстры — Ловаса (англ.) (LLL-алгоритм, L³-алгоритм)
Численные алгоритмы
Смотри также Список разделов численного анализа
- Алгоритм де Кастельяу (англ.) — вычисление кривых Безье
- Методы интерполяции
- Приближенное вычисление решений
- Метод фальшпозиции (англ.) (False position method, regula falsi method) — аппроксимирует корни функции
- Метод Ньютона (метод касательных) — нахождение нулей функций с помощью производной
- Метод секущих (метод хорд) — аппроксимирует корни функции
- Метод градиентов (градиентный спуск) — аппроксимирует решение системы уравнений
- Метод сопряжённого градиента (англ.)
- Алгоритм Гаусса — Ньютона — алгоритм для решения нелинейных уравнений методом наименьших квадратов
- Алгоритм Левенберга — Марквардта — алгоритм для решения нелинейных уравнений методом наименьших квадратов
- Танцующие звенья (англ.) — нахождение всех решений задачи точного покрытия
- Алгоритм де Бора (англ.) — вычисление сплайнов
- Алгоритм Гаусса — Лежандра (англ.) — вычисление цифр числа пи
- Алгоритм суммирования Кахана (англ.) — более аккуратный метод суммирования чисел с плавающей точкой
- Алгоритм MISER (англ.) — моделирование методом Монте-Карло, численное интегрирование
- Функции округления (англ.) — классические способы округления чисел
- Сдвигающий алгоритм корня n-ой степени (англ.) — извлечение корня цифра за цифрой
- Вычисление квадратного корня:
- Алгоритм Герона
- школьный (ручной) алгоритм — аппроксимирует квадратный корень числа
- Алгоритм Риша (англ.)
Алгоритмы оптимизации
- Линейное программирование
- Симплекс-метод
- «Венгерский метод» — решение задач целочисленного линейного программирования
- Метод Мака решения задачи о назначениях
- Алгоритм имитации отжига
- Оптимизация роем частиц (англ.)
- Муравьиные алгоритмы
- Метод ветвей и границ
- Дифференциальная эволюция (англ.)
- Эволюционная стратегия (англ.)
- Метод Нелдера — Мида (downhill simplex method) — алгоритм нелинейной оптимизации
- Всхождение со случайным перезапуском (англ.)
- Стохастическое туннелирование (англ.)
- Алгоритм суммирования подмножеств (англ.)
- Метод перебора
- Метод Фибоначчи поиска экстремума — метод выбора точек для нахождения экстремума функции одной переменной
- Градиентный спуск
- Алгоритм Левенберга — Маркардта — комбинафия метода Ньютона и наискорейшего спуска
- Метод Ньютона в оптимизации, основанный на методе Ньютона поиска корня
- Квазиньютоновские методы — методы, основанные на замене матрицы Гессе её приближением.
- Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (англ.) — квазиньютоновский алгоритм нелинейной оптимизации
Грамматический разбор
- Рекурсивный нисходящий парсер — Нисходящий парсер, подходящий для LL(k)-грамматик
- LL-парсер — Относительно простой алгоритм разбора за линейное время для ограниченного класса контекстно-свободных грамматик
- LR-парсер (англ.) — Более сложный алгоритм разбора за линейное время для большего класса контекстно-свободных грамматик. Варианты:
- Парсер старьёвщика (англ.) — Алгоритм разбора за линейное время поддерживающий некоторые контекстно-свободные грамматики и грамматики разбора выражений
- Алгоритм CYK (англ.) — O(n3)-алгоритм для разбора любой контекстно-свободной грамматики
- Алгоритм Эрли (англ.) — Другой O(n3)-алгоритм для разбора любой контекстно-свободной грамматики
- GLR-парсер (англ.) — алгоритм для разбора любой контекстно-свободной грамматики, он предназначен для определённых грамматик, на которых он действует практически за линейное время и O(n3) в худшем случае.
- Метод рекурсивного спуска — это один из методов определения принадлежности входной строки к некоторому формальному языку, описанному контекстно-свободной грамматикой
- Алгоритм Рутисхаузера — работает в предположении о полной скобочной структуре выражения
Квантовые алгоритмы
Приложения квантовых вычислений к различным категориям проблем и алгоритмы
- Алгоритм Гровера — позволяет выполнять поиск среди N вариантов за
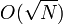 проверок
проверок - Алгоритм Шора — полиномиальный алгоритм факторизации числа
- Алгоритм Дойча — Джоза — критерий баланса для булевой функции
- Задача Фейнмана
Теория вычислений и автоматов
- Конструирование набора подмножеств (англ.) — алгоритм для преобразования недетерминированного автомата в детерминированный
- Алгоритм Тодда — Коксетера — процедура для создания сомножеств
Другие
- Астрономические алгоритмы
- Алгоритм Баума — Велша
- Алгоритмы манипуляции битами
- Алгоритм создания битовой маски
- Алгоритм обмена при помощи исключающего ИЛИ — обмен значений двух переменных без использования буфера
- Алгоритм вычисления дня недели
- Алгоритм Шрейера — Симса (англ.)
- Алгоритм Витерби
- Алгоритм Луна — метод проверки правильности идентификационных чисел
- Алгоритм стемминга — процесс нахождения основы слова
Примечания
Литература
- Ахо, Альфред, В., Хопкрофт, Джон, Ульман, Джеффри, Д. Структуры данных и алгоритмы. — Издательский дом «Вильямс», 2000. — С. 384. — ISBN 5-8459-0122-7 (рус.) / ISBN 0-201-00023-7 (англ.)
- Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. — Москва: МЦНМО, 2003. — С. 328. — ISBN 5-94057-103-4
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Дональд Кнут Искусство программирования, том 2. Получисленные методы = The Art of Computer Programming, vol. 2. Seminumerical Algorithms. — 3-е изд. — М.: «Вильямс», 2007. — С. 832. — ISBN 0-201-89684-2
- Дональд Кнут Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol. 3. Sorting and Searching. — 2-е изд. — М.: «Вильямс», 2007. — С. 824. — ISBN 0-201-89685-0
- Дональд Кнут Искусство программирования, том 4, выпуск 3. Генерация всех сочетаний и разбиений = The Art of Computer Programming, Volume 4, Fascicle 3 : Generating All Combinations and Partitions. — М.: «Вильямс», 2007. — С. 208. — ISBN 0-201-85394-9
- Дональд Кнут Искусство программирования, том 4, выпуск 4. Генерация всех деревьев. История комбинаторной генерации = The Art of Computer Programming, Volume 4, Fascicle 4: Generating All Trees — History of Combinatorial Generation. — М.: «Вильямс», 2007. — С. 160. — ISBN 0-321-33570-8
- Д-р Сидни Фейт TCP/IP: Архитектура, протоколы, реализация (включая IP версии 6 и IP Security) = TCP/IP: Arhitecture, Protocols, and Implementation with IPv6 and IP Security. — 2nd. ed. Dr. Sidnie Feit Copyright 1997, 1993 by The McGraw-Hill Companies, Inc. (включая IP версии 6 и IP Security). — 2-е изд. — М.: Издательство «Лори», 2003. — С. 424. — ISBN 5-85582-072-6 (рус.) / ISBN 0-07-021389-5 (англ.)
- Порублев Илья Николаевич, Ставровский Андрей Борисович Алгоритмы и программы. Решение олимпиадных задач. — М.: «Вильямс», 2007. — С. 480. — ISBN 978-5-8459-1244-2
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Роберт Седжвик Фундаментальные алгоритмы на C. Анализ/Структуры данных/Сортировка/Поиск = Algorithms in C. Fundamentals/Data Structures/Sorting/Searching. — СПб.: ДиаСофтЮП, 2003. — С. 672. — ISBN 5-93772-081-4
- Роберт Седжвик Фундаментальные алгоритмы на C. Алгоритмы на графах = Algorithms in C. Graph Algorithms. — СПб.: ДиаСофтЮП, 2003. — С. 480. — ISBN 5-93772-082-2
- Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh Vazirani Algorithms. — The McGraw-Hill Companies, 2006. — С. 320. — ISBN 0-07-352340-2
Ссылки
- Сайт по методам сжатия данных
- Дискретная математика: Алгоритмы — библиотека алгоритмов и визуализаторов
- Алгоритмы, методы, исходники
Wikimedia Foundation. 2010.
