- Алгоритм Кнута — Морриса — Пратта
-
Алгоритм Кнута — Морриса — Пратта
Алгоритм Кнута — Морриса — Пратта (КМП-алгоритм) — алгоритм поиска образца (подстроки) в строке.
Алгоритм был открыт Д. Кнутом и В. Праттом и, независимо от них, Д. Моррисом[1]. Результаты своей работы они опубликовали совместно в 1977 году.[2]
Постановка задачи
Поставим следующую задачу: имеется образец
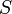 и строка
и строка 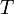 , и нужно определить индекс, начиная с которого строка
, и нужно определить индекс, начиная с которого строка 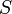 содержится в строке
содержится в строке 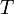 . Если
. Если 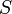 не содержится в
не содержится в 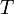 — вернуть индекс, который не может быть интерпретирован как позиция в строке (например, отрицательное число). При необходимости отслеживать каждое вхождение образца в текст имеет смысл завести дополнительную функцию, вызываемую при каждом обнаружении образца.
— вернуть индекс, который не может быть интерпретирован как позиция в строке (например, отрицательное число). При необходимости отслеживать каждое вхождение образца в текст имеет смысл завести дополнительную функцию, вызываемую при каждом обнаружении образца.Описание алгоритма и оценка времени работы
Рассмотрим сравнение строк на позиции
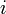 , где образец
, где образец ![\displaystyle S[ 0, m - 1 ]](http://dic.academic.ru/pictures/wiki/files/56/8f505b3c2a680fc50f8edba785ab0fd4.png) сопоставляется с частью текста
сопоставляется с частью текста ![\displaystyle \displaystyle T[ i, i + m - 1 ]](http://dic.academic.ru/pictures/wiki/files/57/949781ee148c72a24c5d0d485ca742d9.png) . Предположим, что первое несовпадение произошло между
. Предположим, что первое несовпадение произошло между ![\displaystyle T[ i + j ]](http://dic.academic.ru/pictures/wiki/files/48/0dc5d51c12571a9d06d8ff99c2cdb323.png) и
и ![\displaystyle S[ j ]](http://dic.academic.ru/pictures/wiki/files/56/81cf1be3adfa3a9fde6f093b7a4745a9.png) , где
, где 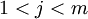 . Тогда
. Тогда ![\displaystyle T[ i, i + j - 1 ] = S[ 0, j - 1 ] = P](http://dic.academic.ru/pictures/wiki/files/57/9256629a525ac4b56aeff9353f63a57b.png) и
и ![\displaystyle a = T[ i + j ] \ne S[ j ] = b](http://dic.academic.ru/pictures/wiki/files/54/65e98042ed8bb5e4689d1bd809b7ea08.png) .
.При сдвиге вполне можно ожидать, что префикс (начальные символы) образца
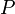 сойдется с каким-нибудь суффиксом (подсловом) текста
сойдется с каким-нибудь суффиксом (подсловом) текста 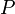 . Длина наиболее длинного префикса, являющегося одновременно суффиксом есть префикс-функция от строки
. Длина наиболее длинного префикса, являющегося одновременно суффиксом есть префикс-функция от строки 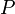 .
.Это приводит нас к следующему алгоритму: пусть
![\displaystyle \rm{\pi}[ j ]](http://dic.academic.ru/pictures/wiki/files/51/36258f8776d511c55cf819c393f7b2f3.png) — префикс-функция от строки
— префикс-функция от строки ![\displaystyle S[ 0, j - 1 ]](http://dic.academic.ru/pictures/wiki/files/54/6700a654ee1752db5958f1d15d7823de.png) . Тогда после сдвига мы можем возобновить сравнения с места
. Тогда после сдвига мы можем возобновить сравнения с места ![\displaystyle T[ i + j ]](http://dic.academic.ru/pictures/wiki/files/48/0dc5d51c12571a9d06d8ff99c2cdb323.png) и
и ![\displaystyle S[ \rm{\pi}[ j ] ]](http://dic.academic.ru/pictures/wiki/files/97/a63fbf1fdcf19d0abb9f50953a40e72a.png) без потери возможного местонахождения образца. Средствами амортизацононного анализа можно показать, что таблица
без потери возможного местонахождения образца. Средствами амортизацононного анализа можно показать, что таблица 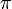 может быть вычислена за
может быть вычислена за 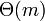 сравнений перед началом поиска. А поскольку строка
сравнений перед началом поиска. А поскольку строка 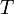 будет пройдена ровно один раз, суммарное время работы алгоритма будет равно
будет пройдена ровно один раз, суммарное время работы алгоритма будет равно 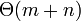 , где n - длина текста
, где n - длина текста 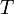 .
.Пример практической реализации
Пусть ищется строка
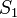 в строке
в строке 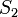 . Построим строку
. Построим строку 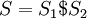 , где символ
, где символ 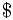 — символ, не встречающийся ни в
— символ, не встречающийся ни в 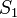 , ни в
, ни в 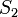 . Далее вычислим значения префикс-функции от строки
. Далее вычислим значения префикс-функции от строки 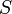 и всех её префиксов. Теперь, если префикс-функция от префикса строки
и всех её префиксов. Теперь, если префикс-функция от префикса строки 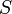 длины
длины 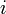 равна
равна 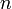 , где
, где 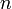 — длина
— длина 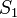 , и
, и 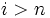 , то в строке
, то в строке 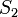 есть вхождение
есть вхождение 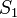 , начиная с позиции
, начиная с позиции 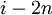 .
.Реализация алгоритма на языке Паскаль (диалект Дельфи 5 и выше)
Function Pos ( const Needle, HayStack : string ) : Integer; var F: array of Integer; k, i: integer; begin SetLength(F, 1+Length(Needle)); // Строки индексируются с 1, открытые массивы с 0. F[1] := 0; k := 0; for i := 2 to Length(Needle) do begin while (k > 0) and (Needle[k+1] <> Needle[i]) do k := F[k]; if Needle[k+1] = Needle[i] then Inc(k); F[i] := k; end; k := 0; for i := 1 to Length(HayStack) do begin while (k > 0) and (Needle[k+1] <> HayStack[i]) do k := F[k]; if Needle[k+1] = HayStack[i] Then Inc(k); if k = Length(Needle) Then begin Result := i-length(Needle)+1; //Здесь обрабатываются полученные данные после того как мы нашли подстроку, //можно сделать результатом работы функции не только положение подстроки Break; end; end; end;
Реализация алгоритма на языке C++
# include <string> # include <vector> using namespace std; string::size_type KMP(const string& S, int begin, const string& pattern){ vector<int> pf (pattern.length()); pf[0] = 0; for (int k = 0, i = 1; i<pattern.length(); ++i){ while(k>0 && pattern[i] != pattern[k]) k = pf[k-1]; if (pattern[i] == pattern[k]) k++; pf[i] = k; } for (int k = 0, i = begin; i<S.length(); ++i){ while ((k>0) && (pattern[k] != S[i])) k = pf[k-1]; if (pattern[k] == S[i]) k++; if (k==pattern.length()) return (i-pattern.length()+1);//либо продолжаем поиск следующих вхождений } return (string::npos); }
Реализация алгоритма на языке Си
int seek_substring_KMP (char s[], char q[]) { int i, j, N, M; N = strlen(s); M = strlen(q); int *d =(int*)malloc(M*sizeof(int)); /* динамический массив длины М*/ /* Вычисление префикс-функции */ i=0; j=-1; d[0]=-1; while(i<M-1) { while((j>=0) && (q[j]!=q[i])) j = d[j]; i++; j++; if(q[i]==q[j]) d[i]=d[j]; else d[i]= j; } /* поиск */ for(i=0,j=0;(i<N)&&(j<M); i++,j++) while((j>=0)&&(q[j]!=s[i])) j=d[j]; free (d); /* освобождение памяти массива d */ if (j==M) return i-j; else /* i==N */ return -1; }
Реализация алгоритма на языке С#
public int FindSubstring(string input, string pattern) { int n = input.Length; int m = pattern.Length; if (0 == n) throw new ArgumentException("String mustn't be empty", "input"); if (0 == m) throw new ArgumentException("String mustn't be empty", "pattern"); int[] d = GetPrefixFunction(pattern); int i, j; for (i = 0, j = 0; (i < n) && (j < m); i++, j++) while ((j >= 0) && (pattern[j] != input[i])) j = d[j]; if (j == m) return i - j; else return -1; } private int[] GetPrefixFunction(string pattern) { int length = pattern.Length; int[] result = new int[length]; int i = 0; int j = -1; result[0] = -1; while (i < length - 1) { while ((j >= 0) && (pattern[j] != pattern[i])) j = result[j]; i++; j++; if (pattern[i] == pattern[j]) result[i] = result[j]; else result[i] = j; } return result; }
Реализация алгоритма на языке Java
void KMP (char[] haystack, char[] needle) { int m = needle.length; int n = haystack.length; int[] pf = new int[m]; pf[0] = -1; //Вычисление префикс-функции for(int i = 1; i < m; i ++) { pf[i] = pf[i - 1] + 1; while(pf[i] > 0 && needle[i - 1] != needle[pf[i] - 1]) pf[i] = pf[pf[i] - 1] + 1; } //Сопоставление образца for(int i = 0, j = 0; i < n; i ++) { while(j > 0 && needle[j] != haystack[i]) j = pf[j]; if(needle[j] == haystack[i]) j ++; if(j == m) { //Образец обнаружен на сдвиге i - m + 1 //Ищем следующее вхождение образца j = pf[j]; } } }
Ссылки
- http://algolist.manual.ru/search/esearch/kmp.php
- Реализация алгоритма КМП на Pascal
- Реализация алгоритма КМП на Java
См. также
Источники
- ↑ Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4
- ↑ Donald Knuth; James H. Morris, Jr, Vaughan Pratt (1977). «Fast pattern matching in strings». SIAM Journal on Computing 6 (2): 323–350. DOI:10.1137/0206024.
Wikimedia Foundation. 2010.
