Число Мерсенна

Число́ Мерсе́нна — числа вида M_n = 2ⁿ - 1, где n — натуральное число. Названы в честь французского математика Мерсенна.

Последовательность чисел Мерсенна начинается так:

1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, ... (последовательность A000225 в OEIS)

Иногда числами Мерсенна называют числа M_p с простыми индексами p. Эта последовательность начинается так:

3, 7, 31, 127, 2047, 8191, 131071, 524287, 8388607, 536870911, 2147483647... (последовательность A001348 в OEIS)

Свойства

• Если M_n является простым, то число n также простое.
• Любой делитель числа M_p для простого p имеет вид 2pk + 1, где k — целое число (следствие малой теоремы Ферма).
• Каждое чётное совершенное число имеет вид M_p(M_p + 1) / 2 = 2^{p − 1}(2^p − 1), где число Мерсенна M_p является простым (доказано Эйлером).

Простые чи́сла Мерсенна

Чи́сла Мерсенна получили известность в связи с эффективным критерием простоты Люка — Лемера, благодаря которому простые чи́сла Мерсенна давно удерживают лидерство как самые больши́е известные простые чи́сла.^[1] На данный момент самым больши́м известным простым числом является число Мерсенна M_43112609 = 2^43112609 − 1, найденное в августе 2008 года в рамках проекта распределённых вычислений M_43112609 составляет 12978189 десятичных цифр, что позволяет GIMPS претендовать на премию в 100000 долларов США, назначенную сообществом Electronic Frontier Foundation за нахождение простого числа длина которого превышает 10 миллионов десятичных цифр.^[2]

Всего известно 46 простых числа́ Мерсенна, причём порядковые номера с уверенностью установлены только у первых 39-ти.^[3] Интересно отметить, что 46-е найденное простое число Мерсенна было найдено на две недели позднее 45-го найденного простого числа Мерсенна и оказалось меньше его.

Последовательность простых чисел Мерсенна и их показателей начинается так:

M_p: 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, ... (последовательность A000668 в OEIS)

p: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, ... (последовательность A000043 в OEIS)

Вариации и обобщения

• Двойные числа Мерсенна определяются как $MM_n = M_{M_n} = 2^{2^n - 1} - 1$.

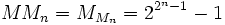Открытые проблемы

• Бесконечность количества простых чисел Мерсенна и их асимптотика
• Простота числа $M_{M_{61}} = 2^{2^{61} - 1} - 1$

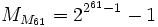
Примечания

1. ↑ The Largest Known Primes(англ.)
2. ↑ EFF Cooperative Computing Awards(англ.)
3. ↑ Mersenne Primes: History, Theorems and Lists(англ.)

Ссылки

• GIMPS
• Weisstein, Eric W. Mersenne Number на сайте Wolfram MathWorld.(англ.)
• Weisstein, Eric W. Double Mersenne Numbers на сайте Wolfram MathWorld.(англ.)