Алгоритм Прима

Алгоритм Прима  — алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые был открыт в 1930 году чешским математиком Войцехом Ярником, позже переоткрыт Робертом Примом в 1957 году, и, независимо от них, Э. Дейкстрой в 1959 году.

Описание

Построение начинается с дерева, включающего в себя одну (произвольную) вершину. В течение работы алгоритма дерево разрастается, пока не охватит все вершины исходного графа. На каждом шаге алгоритма к текущему дереву присоединяется самое лёгкое из рёбер, соединяющих вершину из построенного дерева и вершину не из дерева.

Вход

• Связный неориентированный граф $G(V,E)$

Выход

• Множество T рёбер минимального остовного дерева

Пример

Изображение	Множество выбранных вершин U	Ребро (u,v)	Множество невыбранных вершин V \ U	Описание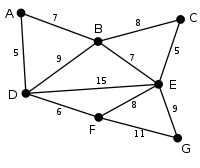
	{}		{A,B,C,D,E,F,G}	Исходный взвешенный граф. Числа возле ребер показывают их веса, которые можно рассматривать как расстояния между вершинами.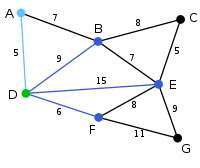
	{D}	(D,A) = 5 V (D,B) = 9 (D,E) = 15 (D,F) = 6	{A,B,C,E,F,G}	В качестве начальной произвольно выбирается вершина D. Каждая из вершин A, B, E и F соединена с D единственным ребром. Вершина A — ближайшая к D, и выбирается как вторая вершина вместе с ребром AD.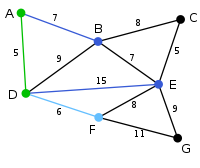
	{A,D}	(D,B) = 9 (D,E) = 15 (D,F) = 6 V (A,B) = 7	{B,C,E,F,G}	Следующая вершина — ближайшая к любой из выбранных вершин D или A. B удалена от D на 9 и от A — на 7. Расстояние до E равно 15, а до F — 6. F является ближайшей вершиной, поэтому она включается в дерево F вместе с ребром DF.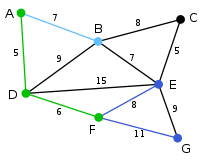
	{A,D,F}	(D,B) = 9 (D,E) = 15 (A,B) = 7 V (F,E) = 8 (F,G) = 11	{B,C,E,G}	Аналогичным образом выбирается вершина B, удаленная от A на 7.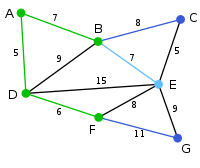
	{A,B,D,F}	(B,C) = 8 (B,E) = 7 V (D,B) = 9 цикл (D,E) = 15 (F,E) = 8 (F,G) = 11	{C,E,G}	В этом случае есть возможность выбрать либо C, либо E, либо G. C удалена от B на 8, E удалена от B на 7, а G удалена от F на 11. E — ближайшая вершина, поэтому выбирается E и ребро BE.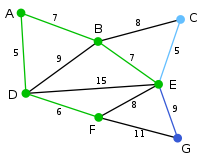
	{A,B,D,E,F}	(B,C) = 8 (D,B) = 9 цикл (D,E) = 15 цикл (E,C) = 5 V (E,G) = 9 (F,E) = 8 цикл (F,G) = 11	{C,G}	Здесь доступны только вершины C и G. Расстояние от E до C равно 5, а до G — 9. Выбирается вершина C и ребро EC.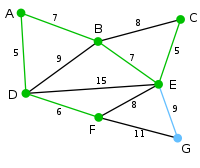
	{A,B,C,D,E,F}	(B,C) = 8 цикл (D,B) = 9 цикл (D,E) = 15 цикл (E,G) = 9 V (F,E) = 8 цикл (F,G) = 11	{G}	Единственная оставшаяся вершина — G. Расстояние от F до нее равно 11, от E — 9. E ближе, поэтому выбирается вершина G и ребро EG.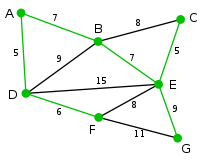
	{A,B,C,D,E,F,G}	(B,C) = 8 цикл (D,B) = 9 цикл (D,E) = 15 цикл (F,E) = 8 цикл (F,G) = 11 цикл	{}	Выбраны все вершины, минимальное остовное дерево построено (выделено зеленым). В этом случае его вес равен 39.

Реализация

Обозначения

• $d[i]$ — расстояние от $i$-й вершины до построенного дерева
• $p[i]$ — предок $i$-й вершины, то есть такая вершина $u$, что $(i,u)$ легчайшее из всех рёбер соединяющее i с вершиной из построенного дерева.
• $w(i,j)$ — вес ребра $(i,j)$
• $Q$ — приоритетная очередь вершин графа, где ключ — $d[i]$
• $T$ — множество ребер минимального остовного дерева

Псевдокод

$T \gets$ {} 
Для каждой вершины  $i \in V$  
 $d[i] \gets \infty$
 $p[i] \gets nil$
$d[1] \gets 0$ 
$Q \gets V$ 
$v \gets\ Extract.min(Q)$ 
Пока $Q$ не пуста
 Для каждой вершины $u$ смежной с $v$
  Если $u \in Q$ и $w(v,u) < d[u]$  
   $d[u] \gets w(v,u)$
   $p[u] \gets v$
 $v \gets Extract.Min(Q)$
 $T \gets T+(p[v],v)$

Оценка

Асимптотика алгоритма зависит от способа хранения графа и способа хранения вершин, не входящих в дерево. Если приоритетная очередь $Q$ реализована как обычный массив $d$, то $Extract.Min(Q)$ выполняется за $O(n)$, а стоимость операции $d[u] \gets w(v, u)$ составляет $O(1)$. Если $Q$ представляет собой бинарную пирамиду, то стоимость $Extract.Min(Q)$ снижается до $O(\log n)$, а стоимость $d[u] \gets w(v,u)$ возрастает до $O(\log n)$. При использовании фибоначчиевых пирамид операция $Extract.Min(Q)$ выполняется за $O(\log n)$, а $d[u] \gets w(v, u)$ за $O(1)$.

Способ представления графа и приоритетной очереди	Асимптотика
Массив d, списки смежности (матрица смежности)	$O(V^2)$
Бинарная пирамида, списки смежности	$O((V + E) \log V) = O(E \log V)$
Фибоначчиева пирамида, списки смежности	$O(E + V \log V)$

См. также

• Алгоритм Краскала

Литература

• V. Jarník: O jistém problému minimálním [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti, 6, 1930, pp. 57–63.  (чешск.)
• R. C. Prim: Shortest connection networks and some generalizations. In: Bell System Technical Journal, 36 (1957), pp. 1389–1401  (англ.)
• D. Cheriton and R. E. Tarjan: Finding minimum spanning trees. In: SIAM Journal on Computing, 5 (Dec. 1976), pp. 724–741  (англ.)
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press, 2009. ISBN 0-262-03384-4. Section 23.2: The algorithms of Kruskal and Prim, pp. 631–638.  (англ.)

Ссылки

• Описание и реализация Алгоритма Прима
• ДИСКРЕТНАЯ МАТЕМАТИКА: АЛГОРИТМЫ : Минимальные остовные деревья