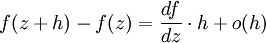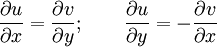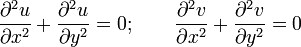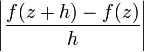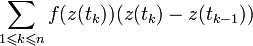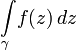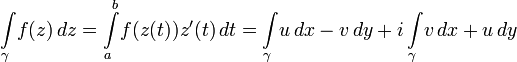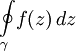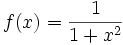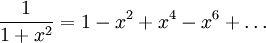- Комплексный анализ (исторический очерк)
-
Ко́мпле́ксный ана́лиз[1][2] или тео́рия фу́нкций ко́мпле́ксного переме́нного (ко́мпле́ксной переме́нной) (ТФКП) — часть математического анализа, в которой рассматриваются и изучаются функции комплексного аргумента.
Содержание
Общие понятия
Для начала отметим, что каждая комплексная функция w = f(z) = f(x + iy) может рассматриваться как пара вещественных функций от двух переменных: f(z) = u(x,y) + iv(x,y), определяющих её вещественную и мнимую часть соответственно. Функции u, v называются компонентами комплексной функции f(z).
Понятие предела функции вводится так же, как и в вещественном случае, с заменой абсолютной величины на комплексный модуль. Если
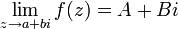 , то
, то 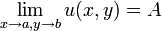 и
и 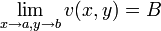 , и обратно.
, и обратно.Непрерывность комплексной функции тоже определяется так же, как в вещественном случае, и она равносильна непрерывности обеих её компонент.
Все основные теоремы о пределе и непрерывности вещественных функций имеют место и в комплексном случае, если это расширение не связано со сравнением комплексных величин на больше-меньше. Например, нет аналога теореме о промежуточных значениях непрерывной функции.
Дифференцирование
Определение
Производная для комплексной функции одного аргумента w = f(z) определяется так же, как и для вещественной:
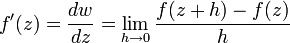 .
.
(здесь h — комплексное число). Если этот предел существует, функция называется дифференцируемой или голоморфной. При этом
Следует учитывать одну важную особенность: поскольку комплексная функция задана на плоскости, существование приведённого предела означает, что он одинаков при стремлении к z с любого направления. Этот факт накладывает существенные ограничения на вид функций-компонент u,v и определяет их жёсткую взаимосвязь (условия Коши — Римана):
Другими словами, гладкость u и v не гарантирует дифференцируемости самой функции.
Более того, имеют место следующие свойства, отличающие комплексный анализ от вещественного:
- Всякая дифференцируемая в некоторой окрестности точки z комплексная функция дифференцируема неограниченное число раз и аналитична в этой окрестности.
- Обе компоненты дифференцируемой комплексной функции являются гармоническими функциями, то есть удовлетворяют уравнению Лапласа:
- Любая гармоническая функция может быть как вещественной, так и мнимой компонентой дифференцируемой функции. При этом другая компонента определяется однозначно (из условий Коши-Римана), с точностью до константы-слагаемого.
Таким образом, любая дифференцируемая комплексная функция — это функция вида u + iv, где u,v — взаимосвязанные гармонические функции двух аргументов.
Геометрический смысл
Каждая комплексная функция w = f(z) = u(x,y) + iv(x,y) определяет некоторое отображение комплексной плоскости (x,y) на другую комплексную плоскость с координатами u,v. При этом выражение:
при малом h геометрически можно истолковать как коэффициент растяжения, которое выполняет данное отображение при переходе от точки z к точке z + h. Тогда существование предела этого выражения, то есть модуля производной, означает, что коэффициент растяжения одинаков в любом направлении от точки z.
Что касается аргумента производной, то он определяет угол поворота гладкой кривой, проходящей через точку z. Все гладкие кривые при таком отображении поворачиваются на один и тот же угол. Отображения, сохраняющие углы, называются конформными; таким образом, любая дифференцируемая комплексная функция определяет конформное отображение (в той области, где её производная не обращается в ноль). С этим фактом связано широкое применение комплексных функций в картографии и гидродинамике[3].
Интегрирование
Понятие первообразной комплексной функции (неопределённого интеграла) вводится так же, как в вещественном случае. Однако аналог определённого интеграла в интервале от a до b на комплексной плоскости не существует, так как путь от начальной точки до конечной неоднозначен. Поэтому основным видом комплексного интеграла является криволинейный интеграл, зависящий от конкретного пути.
Пусть уравнение
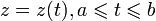 определяет некоторую кусочно-гладкую кривую γ в комплексной плоскости, а функция
определяет некоторую кусочно-гладкую кривую γ в комплексной плоскости, а функция 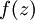 определена в точках этой кривой. Разделим интервал задания параметра на n равных частей:
определена в точках этой кривой. Разделим интервал задания параметра на n равных частей: 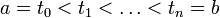 и рассмотрим интегральную сумму:
и рассмотрим интегральную сумму:Предел этой суммы при неограниченном возрастании n называется (комплексным) интегралом по кривой γ от данной функции f(z); он обозначается:
Для любой функции f(z), непрерывной вдоль γ, этот интеграл существует и может быть вычислен через обычный вещественный интеграл по параметру:
Здесь u,v — компоненты f(z).
Если кривая γ образует замкнутый контур (то есть конечная точка пути совпадает с начальной), употребляется особое обозначение интеграла:
Имеет место важная интегральная теорема Коши: для любой функции f(z), аналитической в односвязной области
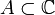 и для любой замкнутой кривой
и для любой замкнутой кривой 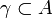 справедливо соотношение
справедливо соотношение 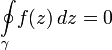 . Другие мощные инструменты для вычисления комплексных и вещественных интегралов:
. Другие мощные инструменты для вычисления комплексных и вещественных интегралов:Приложения в вещественном анализе
С помощью теории вычетов, являющейся частью ТФКП, вычисляются многие сложные интегралы по замкнутым контурам.
Средствами комплексного анализа объясняются некоторые моменты, не поддающиеся простой интерпретации в терминах вещественного анализа. Приведем классический пример: функция
непрерывна и бесконечно дифференцируема на всей вещественной прямой. Рассмотрим её ряд Тейлора
Этот ряд сходится только в интервале ( − 1;1), хотя точки
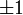 не являются какими-то особенными для f(x).
не являются какими-то особенными для f(x).Положение проясняется при переходе к функции комплексного переменного
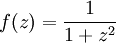 , у которой обнаруживаются две особые точки:
, у которой обнаруживаются две особые точки: 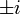 . Соответственно, эту функцию можно разложить в ряд Тейлора только в круге
. Соответственно, эту функцию можно разложить в ряд Тейлора только в круге 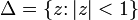 .
.История
Фундаментальные работы в комплексном анализе связаны с именами Римана, Коши, Вейерштрасса и многих других известных математиков. Теория конформных отображений стала бурно развиваться благодаря имеющимся примененениям в инженерном деле, также методы и результаты комплексного анализа применяются в аналитической теории чисел. Новый всплеск интереса к комплексному анализу связан с комплексной динамикой и теорией фракталов.
См. также
- Аналитическая функция
- Голоморфная функция
- Комплексные числа
- Кватернионный анализ
- Многомерный комплексный анализ
Примечания
- ↑ Школьная энциклопедия «Математика». Издательство «Большая Российская энциклопедия». 1996 год. Гл. ред. С.М. Никольский.
- ↑ «Русский орфографический словарь» Российской академии наук под ред. В. В. Лопатина указывает ударение компле́ксный, ряд других словарей допускают оба варианта ударения, см. ГРАМОТА.РУ
- ↑ О применении конформных отображений в гидродинамике см.: Лаврентьев М. А., Шабат Б. В. Проблемы гидродинамики и их математические модели. — М.: Наука, 1973.
Литература
- История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд.. — М.: Наука, 1972.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 2001. — Т. II, глава XII, §5. — 800 с. — ISBN 5-9221-0155-2
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969.
Wikimedia Foundation. 2010.