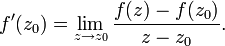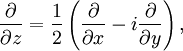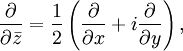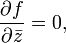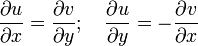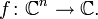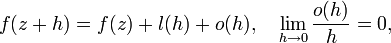- Регулярная функция
-
Голоморфная функция — комплекснозначная функция, определённая на открытом подмножестве комплексной плоскости
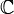 и комплексно дифференцируемая в каждой точке.
и комплексно дифференцируемая в каждой точке.В отличие от вещественного случая, это условие влечёт, что функция бесконечно дифференцируема и может быть представлена сходящимся к ней рядом Тейлора.
Голоморфные функции также называют иногда аналитическими, хотя второе понятие гораздо более широкое, так как аналитическая функция не обязана быть определена на множестве комплексных чисел. Тот факт, что для комплекснозначных функций комплексной переменной множества голоморфных и аналитических функций совпадают, является нетривиальным и весьма замечательным результатом комплексного анализа.
Содержание
Определение
Пусть U — открытое подмножество в
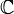 и
и 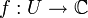 — комплекснозначная функция на U.
— комплекснозначная функция на U.- Функцию f называют комплексно дифференцируемой в точке
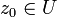 , если существует предел
, если существует предел
- В этом выражении предел берется по всем последовательностям комплексных чисел, сходящихся к z0, для всех таких последовательностей выражение должно сходиться к одному и тому же числу f'(z0). Комплексное дифференцирование во многом похоже на вещественное: оно линейно и удовлетворяет тождеству Лейбница.
- Функцию f называют голоморфной в U, если она комплексно дифференцируема в каждой точке U.
- Функцию f называют голоморфной в
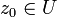 , если она голоморфна в некоторой окрестности z0.
, если она голоморфна в некоторой окрестности z0.
Другое определение
Определению голоморфной функции можно придать несколько другой вид, если воспользоваться операторами
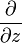 и
и 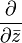 , определяемыми по правилу
, определяемыми по правилугде z = x + iy. Тогда функция f называется голоморфной, если
что эквивалентно условиям Коши — Римана.
Связанные определения
- Целая функция — функция, голоморфная на всей комплексной плоскости.
- Мероморфная функция — функция, голоморфная в области
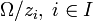 и имеющая во всех своих особых точках zi полюс.
и имеющая во всех своих особых точках zi полюс. - Функция f называется голоморфной на компакте K, если существует открытое множество D, содержащее K, такое что f голоморфна в D.
Свойства
- Комплексная функция u + iv = f(x + iy) является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана
- и частные производные
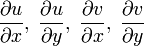 непрерывны.
непрерывны.
- Сумма и произведение голоморфных функций — голоморфная функция, что следует из линейности дифференцирования и выполнения правила Лейбница. Частное голоморфных функций также голоморфно во всех точках, где знаменатель не обращается в 0.
- Производная голоморфной функции опять является голоморфной, поэтому голоморфные функции являются бесконечно дифференцируемыми в своей области определения.
- Голоморфные функции являются аналитическими, то есть могут быть представлены в виде сходящегося в некоторой окрестности каждой точки ряда Тейлора. Таким образом, для комплексных функций комплексной переменной множества голоморфных и аналитических функций совпадают.
- Из любой голоморфной функции можно выделить её вещественную и мнимую часть, каждая из которых будет решением уравнения Лапласа в
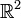 . То есть если
. То есть если 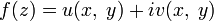 — голоморфная функция, то u и v — гармонические функции.
— голоморфная функция, то u и v — гармонические функции. - Если абсолютная величина голоморфной функции достигает локального максимума во внутренней точке своей области определения, то функция постоянна (предполагается, что область определения связна). Отсюда следует, что максимум и минимум абсолютной величины голоморфной функции могут достигаться лишь на границе области.
- В области, где первая производная голоморфной функции не обращается в 0, а функция однолистна, она осуществляет конформное отображение.
- Интегральная формула Коши связывает значение функции во внутренней точке области с её значениями на границе этой области.
- С алгебраической точки зрения, множество голоморфных на открытом множестве функций — это коммутативное кольцо и комплексное линейное пространство. Это локально выпуклое топологическое векторное пространство с полунормой, равной супремуму на компактных подмножествах.
История
Термин «голоморфная функция» был введён двумя учениками Коши, Брио (1817—1882) и Боке (1819—1895), и происходит от греческих слов őλoς (холос), что значит «целый», и μoρφń (морфе) — форма, образ.[1]
Сегодня многие математики предпочитают термин «голоморфная функция» вместо «аналитическая функция», так как второе понятие более общее. Кроме того, одним из важных результатом комплексного анализа является то, что любая голоморфная функция является аналитической, что не очевидно из определения. Термин «аналитический» употребляют обычно для более общих функций, заданных не обязательно на комплексной плоскости.
Вариации и обобщения
Многомерный случай
Существует также определение голоморфности функций многих комплексных переменных
Для определения используются понятия
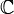 -дифференцируемости и
-дифференцируемости и 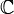 -линейности таких функций
-линейности таких функцийС-линейность
Функция f называется
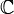 -линейной если удовлетворяются условия:
-линейной если удовлетворяются условия: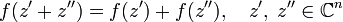 .
.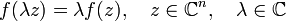
(для
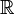 -линейных функций
-линейных функций 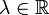 ).
).- Для любой
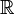 -линейной функции f существуют последовательности
-линейной функции f существуют последовательности 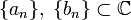 , такие, что
, такие, что 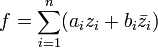 .
. - Для любой
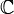 -линейной функции f существуют последовательность
-линейной функции f существуют последовательность 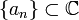 , такая, что
, такая, что 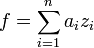 .
.
С-дифференцируемость
Функция f называется
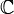 -дифференцируемой в точке
-дифференцируемой в точке 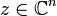 если существуют функции l и o, такие что в окрестности точки z
если существуют функции l и o, такие что в окрестности точки zгде l —
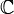 -линейная (для
-линейная (для 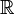 -дифференцируемости —
-дифференцируемости — 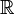 -линейная) функция.
-линейная) функция.Голоморфность
Функция f называется голоморфной в области D, если она
 -дифференцируема в окрестности каждой точки этой области.
-дифференцируема в окрестности каждой точки этой области.Ссылки
- ↑ Markushevich A. I., Silverman, Richard A. (ed.) Theory of functions of a Complex Variable. — М.: Американское математическое общество, 2-е изд. — ISBN 0-8218-3780-X, [1].
Литература
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.
См. также
- Функцию f называют комплексно дифференцируемой в точке
Wikimedia Foundation. 2010.