РАЦИОНАЛЬНАЯ ФУНКЦИЯ

1) Р. ф.- функция w=R(z), где R(z) - рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек-рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф. можно записать (не единственным образом) в виде

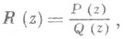
где Р, Q - многочлены, . Коэффициенты этих многочленов наз. к о э ф ф и ц и е н т а м и Р. ф. Дробь P/Qназ. несократимой, если Р, Q не имеют общих нулей (то есть Р, Q - взаимно простые многочлены). Всякую Р. ф. можно записать в виде несократимой дроби R(z)=P(z)/Q(z);если при этом Р имеет степень m, a Q - степень п, то степенью Р. ф. R(z)наз. пару (m, n) или число

Р. ф. степени ( т, п).при n=0, т. е. многочлен, наз. ц е л о й р а ц и о н а л ь н о й ф у н к ц и е й, в противном случае - д р о б н о - р а ц и о н а л ь н о й ф у н к ц и е й. Р. ф. не имеет степени. При m<n дробь Rназ. правильной, при - неправильной. Неправильную дробь можно единственным образом записать в виде

где Р ₁ -многочлен, наз. целой частью дроби Р/Q, a P₂/Q- правильная дробь. Правильная дробь с несократимой записью R(z)=P (z)/Q(z), где

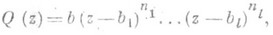
может быть единственным образом разложена в сумму простейших дробей:

(1)

Если P(x)/Q(x)-- правильная Р. ф. с действительными коэффициентами и

где - действительные числа, , то P(x)/Q(x)также единственным образом представляется в виде

(2)

где все коэффициенты действительны. Эти коэффициенты, как и в (1), могут быть найдены неопределенных коэффициентов методом.

Р. ф. степени (m, п).в несократимой записи определена и аналитична в расширенной комплексной плоскости (т. е. плоскости, дополненной точкой ) за исключением конечного числа особых точек- полюсов в нулях ее знаменателя, а при т>п еще и в точке 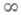; при этом сумма кратностей полюсов функции Rравна ее степени N. Обратно, всякая аналитич. ция, имеющая в расширенной комплексной плоскости в качестве особых точек только полюсы, является Р. ф.

В результате арифметич. действий над. Р. ф. получают также Р. ф. (деление на исключается), так что все Р. ф. образуют поле; вообще, Р. ф. с коэффициентами из нек-рого поля образуют поле. Если R₁(z), R₂(z) суть Р. ф., то и R₁(R₂(z))является Р. ф. Производная порядка рот Р. ф. степени N есть Р. ф. степени 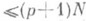. Неопределенный интеграл (первообразная) от Р. ф. представляет собой сумму нек-рой Р. ф. и выражений вида . Если Р. ф. R(х)действительна при действительном х, то неопределенный интеграл может быть записан в виде суммы нек-рой Р. ф. R₀(x)с действительными коэффициентами, выражений вида

и произвольной постоянной С(здесь числа 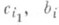, 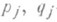- те же, что и в (2), M_j, N_j - нек-рые действительные числа). Функцию R₀(x)по Остроградского методу можно найти, минуя разложение R(х)на простейшие дроби (2).

Удобные для вычислений, Р. ф. используются для приближенного представления функций. Рассматриваются также Р. ф. от нескольких действительных или комплексных переменных R = P/Q, где Р, Q - многочлены от соответствующих переменных , а также абстрактные Р. ф.

где Ф ₁, Ф ₂, ... - линейно независимая система непрерывных функций на нек-ром бикомпакте X, а A₁,..., А _т, B₁, . . ., B _п - числа.

См. также Дробно-линейная функция, Жуковского функция.

Лит.:[1] П р и в а л о в И. И., Введение в теорию функций комплексного переменного, 12 изд., М., 1977; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд., М., 1975. Е. П. Долженко.

2)Р. ф. н а а л г е б р а и ч е с к о м м н о г о о бр а з и и - обобщение классич. понятия рациональной функции (см. п. 1). Р. ф. на неприводимом алгебраич. многообразии X - это класс эквивалентности пар (U, f), где X- непустое открытое подмножество в X, а f - регулярная функция на U. Две пары (U, f) и (V, g )наз. эквивалентными, если f=g на . Р. ф. на Xобразуют поле, обозначаемое k(X).

В случае, когда X=Spec R - аффинное неприводимое многообразие, поле Р. ф. на Xсовпадает с полем частных кольца R. Степень трансцендентности над kполя k(X). наз. р а з м е р н о с т ь ю м н о г о о бр а з и я X.

Лит.:[1] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972. Вик. С. Куликов.