Решетка (теория множеств)

Решётка, структура — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.

Примеры

1. множество всех подмножеств данного множества, упорядоченное по включению;
2. всякое линейно упорядоченное множество; причём если 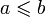$a\leqslant b$, то $\sup(a,b) = b, \inf(a,b) = a$;
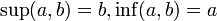3. множество всех подпространств векторного пространства, упорядоченных по включению, где 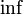$\inf$ — пересечение, а 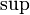$\sup$ — сумма соответствующих подпространств;
4. множество всех неотрицательных целых чисел, упорядоченных по делимости: 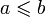$a\leqslant b$, если b = ac для некоторого c. Здесь 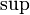$\sup$ — наименьшее общее кратное, а 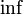$\inf$ — наибольший общий делитель данных чисел;
5. действительные функции, определённые на отрезке [0, 1], упорядоченные условием 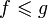$f\leqslant g$, если 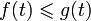$f(t)\leqslant g(t)$ для всех $t\in [0,1]$. Здесь

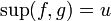$\sup(f,g) = u$, где u(t) = max(f(t),g(t)).

Алгебраическое определение

Решётка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются + и ∙ или $\lor$ и $\land$), удовлетворяющая следующим тождествам

1. a + a = a
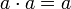   $a\cdot a = a$ (идемпотентность)
2. a + b = b + a
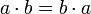   $a\cdot b = b\cdot a$ (коммутативность)
3. (a + b) + c = a + (b + c)
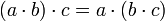   $(a\cdot b)\cdot c = a\cdot (b\cdot c)$ (ассоциативность)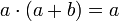
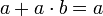4. $a\cdot (a+b) = a$
   $a+a\cdot b = a$ (поглощение).

Связь между этими двумя определениями устанавливается при помощи формул:

a + b = sup(a,b), $a\cdot b = \inf(a,b)$,

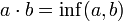и обратно. При этом для любых элементов a и b эквивалентны следующие утверждения:

$a\leqslant b$;

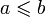ab = a;

a + b = b.

Понятия изоморфизма решёток как универсальных алгебр и как частично упорядоченных множеств совпадают. Однако произвольное изотонное отображение решётки R в решётку R' не обязано быть гомоморфизмом этих решёток как универсальных алгебр.

Связанные определения

• Подрешётка ― подмножество элементов решётки, замкнутое относительно операций + и $\cdot$

История

Появление понятия «решётка» относится к середине XIX века. Чётко его сформулировал Р. Дедекинд в работах 1894 и 1897 годов. Термин «lattice», переведённый как «структура» был введён Биркгофом в 1933 году. В настоящее время в русской терминологии (из-за многозначности слова «структура») он вытеснен переводом «решётка». Исторически роль теории решёток объясняется тем, что многие факты, касающиеся множества идеалов кольца и множества нормальных подгрупп группы, выглядят аналогично и могут быть доказаны в рамках теории дедекиндовых решёток. Как самостоятельное направление алгебры эта теория сформировалась в 30-х годах XX века. Наиболее важные классы решёток, кроме дедекиндовых, — это полные решётки, дистрибутивные решётки и булевы алгебры.

См. также

• Анализ формальных понятий

Ссылки

Доступные бесплатно в интернете монографии:

• Burris, Stanley N., H.P. Sankappanavar A Course in Universal Algebra. — Springer-Verlag, 1981. ISBN 3-540-90578-2.
• Peter Jipsen, Henry Rose Varieties of Lattices — Lecture Notes in Mathematics 1533, Springer Verlag, 1992. ISBN 0-387-56314-8.

Элементарные тексты для обладающих малой математической культурой:

• Thomas Donnellan Lattice Theory. — Pergamon, 1968.
• G. Grätzer Lattice Theory: First concepts and distributive lattices. — W. H. Freeman, 1971.

Обычные введения в предмет, несколько более сложные, чем указанный выше:

• B.A. Davey, H. A. Priestley Introduction to Lattices and Order. — Cambridge University Press, 2002.

Продвинутые монографии:

• Garrett Birkhoff Lattice Theory. — 3rd ed. Vol. 25 of AMS Colloquium Publications. American Mathematical Society, 1967.
• Robert P. Dilworth, Peter Crawley Algebraic Theory of Lattices. — Prentice-Hall, 1973. ISBN 9780130222695.

О свободных решётках:

• R. Freese, J. Jezek, J. B. Nation Free Lattices. — Mathematical Surveys and Monographs Vol. 42. Mathematical Association of America, 1985.
• P.T. Johnstone Stone spaces. — Cambridge Studies in Advanced Mathematics 3. Cambridge University Press, 1982.

Литература

• Биркгоф Г. Теория структур. — пер. с англ., М., 1952;
• Скорняков Л. А. Элементы теории структур. — М., 1970;
• Житомирский Г. И. в сборнике: Упорядоченные множества и решётки. — в. 7, Саратов, 1981;
• Гретцер Г. Общая теория решёток. — пер. с англ., М., 1982.