- ПОЛУУПОРЯДОЧЕННОЕ ПРОСТРАНСТВО
общее название векторных пространств, в к-рых определено бинарное отношение частичного порядка, согласованное определенным образом с векторной структурой пространства. Введение порядка в функциональных пространствах позволяет исследовать в общих рамках функционального анализа такие задачи, к-рые существенно связаны с неравенствами между функциями, с выделением классов положительных функций. Однако, в отличие от множества действительных чисел, допускающего полное упорядочение, естественный порядок в функциональных пространствах оказывается лишь частичным; напр., в пространстве С[a, b] естественно считать, что функция f мажорирует функцию g, если f(t)]
 g(t).при всех
g(t).при всех 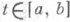 . Но при таком определении порядка многие функции окажутся несравнимыми между собой.
. Но при таком определении порядка многие функции окажутся несравнимыми между собой.
Упорядоченные векторные пространства (у. в. п.). Векторное пространство X над полем действительных чисел наз. упорядоченным, если в нем определено бинарное отношение порядка, причем
 влечет
влечет  для любого
для любого 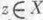 и
и 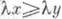 для любого числа
для любого числа  . Таково, напр., С[ а, b]с естественным порядком. Если отношение
. Таково, напр., С[ а, b]с естественным порядком. Если отношение  есть порядок, то множество X+=
есть порядок, то множество X+= - конус, наз. положительным конусом. Обратно, если в векторном пространстве Xзадан конус К с вершиной в нуле, то в Xможет быть введен такой порядок, при к-ром X+=К:следует положить
- конус, наз. положительным конусом. Обратно, если в векторном пространстве Xзадан конус К с вершиной в нуле, то в Xможет быть введен такой порядок, при к-ром X+=К:следует положить  , если
, если  . Рассматриваются и более общие у. в. п., и к-рых определена лишь структура квазипорядка. В этом случае множество Х + есть клин, а всякий клин с вершиной в нуле порождает в Xквазипорядок.
. Рассматриваются и более общие у. в. п., и к-рых определена лишь структура квазипорядка. В этом случае множество Х + есть клин, а всякий клин с вершиной в нуле порождает в Xквазипорядок.
Пусть у. в. и. Xнаделено порядком. Конус Х + наз. воспроизводящим, если X+ -Х +=Х. Это свойство конуса Х + необходимо и достаточно, для того чтобы любое конечное подмножество из Xбыло ограниченным (сверху и снизу). Те у. в. п., в к-рых всякое ограниченное сверху множество имеет верхнюю грань, иначе - точную верхнюю границу, или супремум (а тогда и всякое ограниченное снизу множество имеет нижнюю грань, иначе - точную нижнюю границу, или инфимум), наз. порядково полными или (о)-полными. Более слабый вид полноты в у. в. п. определяется следующим образом: у. в. п. наз. дедекиндово полным, если всякое его ограниченное сверху и направленное вверх подмножество имеет верхнюю грань (множество
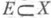 направлено вверх, если для любых
направлено вверх, если для любых  существует такой
существует такой 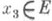 , что
, что  ). Если это требование выполнено для ограниченных возрастающих последовательностей, то у. в. п. наз. дедекиндово (о)-полным. Дедекиндова полнота слабее (о)-полноты. Напр., если X- произвольное бесконечномерное банахово пространство,
). Если это требование выполнено для ограниченных возрастающих последовательностей, то у. в. п. наз. дедекиндово (о)-полным. Дедекиндова полнота слабее (о)-полноты. Напр., если X- произвольное бесконечномерное банахово пространство, 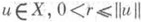 , а К - конус натянутый на замкнутый шар S(и; r).и элемент 0, и с помощью Кв Xвведен порядок, то X- дедекиндово полное, но не (о)-полное. У. в. п. наз. архимедовым, если в нем выполнена Архимеда аксиома. В частности, архимедовым является всякое дедекиндово (о)-полное у. в. п.
, а К - конус натянутый на замкнутый шар S(и; r).и элемент 0, и с помощью Кв Xвведен порядок, то X- дедекиндово полное, но не (о)-полное. У. в. п. наз. архимедовым, если в нем выполнена Архимеда аксиома. В частности, архимедовым является всякое дедекиндово (о)-полное у. в. п.
В у. в. п. вводится понятие порядковой сходимости: последовательность { х п}(о)-сходится к элементу
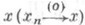 , если существуют такие возрастающая и убывающая последовательности { у п}. и {zn}, что
, если существуют такие возрастающая и убывающая последовательности { у п}. и {zn}, что  и sup yn=x=int zn. (о)-предел обладает многими свойствами предела в множестве действительных чисел, однако нек-рые из них справедливы лишь в архимедовых у. в. п.
и sup yn=x=int zn. (о)-предел обладает многими свойствами предела в множестве действительных чисел, однако нек-рые из них справедливы лишь в архимедовых у. в. п.
Линейный оператор А, действующий из у. в. п. Xв у. в. п. Y(в частности, линейный функционал с действительными значениями), наз. положительным, если
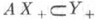 . Для положительных функционалов справедлива следующая теорема о распространении. Пусть Е - линейное подмножество в X, мажорирующее конус X+ (это означает, что для любого
. Для положительных функционалов справедлива следующая теорема о распространении. Пусть Е - линейное подмножество в X, мажорирующее конус X+ (это означает, что для любого 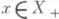 существует такой
существует такой 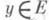 , что
, что 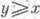 ). Всякий линейный функционал, заданный на Еи положительный относительно конуса
). Всякий линейный функционал, заданный на Еи положительный относительно конуса 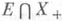 , допускает линейное положительное распространение на все X.
, допускает линейное положительное распространение на все X.
Векторная решетка (в. р.) - у. в. п., в к-ром отношение порядка определяет структуру решетки. При этом для определения в. р. достаточно постулировать для любых двух элементов из у. в. п. существование одной из граней: верхней
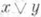 или нижней
или нижней  . Напр., если существует
. Напр., если существует 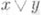 , то
, то  . Если X - в. р., то конус X+ наз. миниэдральным. В в. р. для любого ее элемента хсуществуют положительная и отрицательная части:
. Если X - в. р., то конус X+ наз. миниэдральным. В в. р. для любого ее элемента хсуществуют положительная и отрицательная части: 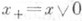 и
и 
При этом x=x+-x-, и эта формула дает "минимальное" представление хв виде разности положительных элементов, т. е. если х=у-z, где
 то
то  ,
,  . Миниэдральный конус является воспроизводящим. Элемент | х|=х ++х - ваз. модулем элемента х. В пространстве С[ а, b] с естественным упорядочением положительный конус миниэдрален, положительная часть любой функции x(t).из Сполучается из x(t).заменой ее отрицательных значений нулем, а модуль есть функция |x(t)|. В в, р. всякое конечное множество элементов имеет обе грани. Модуль элемента в. р. обладает многими свойствами абсолютной величины действительного числа.
. Миниэдральный конус является воспроизводящим. Элемент | х|=х ++х - ваз. модулем элемента х. В пространстве С[ а, b] с естественным упорядочением положительный конус миниэдрален, положительная часть любой функции x(t).из Сполучается из x(t).заменой ее отрицательных значений нулем, а модуль есть функция |x(t)|. В в, р. всякое конечное множество элементов имеет обе грани. Модуль элемента в. р. обладает многими свойствами абсолютной величины действительного числа.
В. р. наз. дистрибутивной, если для произвольного множества ее элементов {х a}, у к-рого существует sup х a при любом
 справедлива формула: у
справедлива формула: у  . Тогда верна и двойственная формула:
. Тогда верна и двойственная формула: 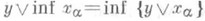
Теорема о двойном разбиении положительных элементов: если x=y+z, где
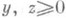 , и одновременно х=х 1+...+х n, где все
, и одновременно х=х 1+...+х n, где все 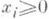 , то каждый х i можно представить в виде xi= у i+zi так, что все
, то каждый х i можно представить в виде xi= у i+zi так, что все  и что
и что
y=y1+...+y п, z=z1+...+zn.
Два элемента х, у в. р. наз. дизъюнктными (xdy), если
 . Два множества А , В наз. дизъюнктными, если adb для любых
. Два множества А , В наз. дизъюнктными, если adb для любых  . В пространстве С[ а, b]дизъюнктность xdy означает, что
. В пространстве С[ а, b]дизъюнктность xdy означает, что 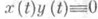 . Положительный элемент еназ. слабой единицей (единицей в смысле Фрейденталя), если 0 - единственный элемент, дизъюнктный с е. В С[ а, b]слабой единицей является любая функция, к-рая больше 0 на всюду плотном множестве. Если же элемент етаков, что для любого хсуществует l, при к-ром
. Положительный элемент еназ. слабой единицей (единицей в смысле Фрейденталя), если 0 - единственный элемент, дизъюнктный с е. В С[ а, b]слабой единицей является любая функция, к-рая больше 0 на всюду плотном множестве. Если же элемент етаков, что для любого хсуществует l, при к-ром  , то еназ. сильной единицей, а Xс сильной единицей наз. в. р. ограниченных элементов. В С[ а, b]сильная единица - любая функция, для к-рой min z(t)>0. Если в архимедовой в. р. Xс сильной единицей еположить
, то еназ. сильной единицей, а Xс сильной единицей наз. в. р. ограниченных элементов. В С[ а, b]сильная единица - любая функция, для к-рой min z(t)>0. Если в архимедовой в. р. Xс сильной единицей еположить  , то Xстановится нормированной решеткой.
, то Xстановится нормированной решеткой.
На плоскости любой конус, кроме одномерного (т. е. луча), миниэдрален. Но в пространствах с большим числом измерений среди замкнутых конусов много не миниэдральных, напр, таковы все "круглые" конусы в R3. Для того чтобы конус (с вершиной в нуле) в n-мерном архимедовом у. в. п. был миниэдральным, необходимо и достаточно, чтобы он был натянут на ( п-1)-мерный симплекс с линейно независимыми вершинами. Всякая архимедова n-мерная в. р. изоморфна пространству Rn с покоординатным упорядочением.
К-пространства (К.-п.), пространства Канторовича, суть (о)-полные в. р. Это - основной класс П. п., они всегда архимедовы, (о)-сходимость в К.-п. описывается с помощью верхнего и нижнего пределов,
 именно, для огранич. последовательности {xn} и тогда
именно, для огранич. последовательности {xn} и тогда 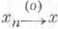 означает, что
означает, что 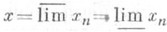 . Пусть Xесть К.-н. Для любого множества
. Пусть Xесть К.-н. Для любого множества 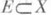 его дизъюнктным дополнением наз. множество
его дизъюнктным дополнением наз. множество 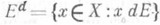 Всякое множество, к-рое является дизъюнктным дополнением (к какому-либо множеству), наз. полосой. Для любого множества Есуществует наименьшая полоса, содержащая Е, именно Edd;она наз. полосой, порожденной множеством Е. Если само Еесть полоса, то Edd=E. Полоса, порожденная одноэлементным множеством, наз. главной. Понятие, полосы вводится и в любой в. р., однако в К.-п. оно играет особую роль, поскольку справедлива теорема о проектировании на полосу: если Е - полоса в X, то для любого
Всякое множество, к-рое является дизъюнктным дополнением (к какому-либо множеству), наз. полосой. Для любого множества Есуществует наименьшая полоса, содержащая Е, именно Edd;она наз. полосой, порожденной множеством Е. Если само Еесть полоса, то Edd=E. Полоса, порожденная одноэлементным множеством, наз. главной. Понятие, полосы вводится и в любой в. р., однако в К.-п. оно играет особую роль, поскольку справедлива теорема о проектировании на полосу: если Е - полоса в X, то для любого  существует единственное разложение x=y+z, где
существует единственное разложение x=y+z, где 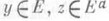 . Определенный при этом линейный оператор у=Рr Е х наз. проектором на полосу Е. Если задана произвольная совокупность попарно дизъюнктных полос Е a, полная в той смысле, что 0 - единственный элемент из X, дизъюнктный всем Е a, то любой
. Определенный при этом линейный оператор у=Рr Е х наз. проектором на полосу Е. Если задана произвольная совокупность попарно дизъюнктных полос Е a, полная в той смысле, что 0 - единственный элемент из X, дизъюнктный всем Е a, то любой 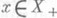 представим в виде х= sup xa, где
представим в виде х= sup xa, где  . Всякий l-идеал
. Всякий l-идеал  также является К.-п. Однако если
также является К.-п. Однако если 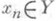 и
и 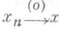 в X, то это соотношение верно и в Y только в том случае, когда последовательность {х п} ограничена в Y.
в X, то это соотношение верно и в Y только в том случае, когда последовательность {х п} ограничена в Y.
Примером К.-п. служит пространство Sвсех действительных почти всюду конечных измеримых функций на [0, 1], в к-ром эквивалентные функции отождествляются. Функция
 считается положительной, если x(t)
считается положительной, если x(t) 0почти всюду. Если А={х п} - счетное ограниченное сверху подмножество из S(ограниченность сверху означает, что существует такая
0почти всюду. Если А={х п} - счетное ограниченное сверху подмножество из S(ограниченность сверху означает, что существует такая  , что
, что  почти всюду для любого п), то функция x(t) = sup xn(t).и будет верхней гранью множества А, т. е. sup Авычисляется поточечно. Однако для несчетных множеств вычисление граней таким же способом уже невозможно, и существование у несчетных множеств ограниченных множеств в Sустанавливается сложнее, (о)-сходимость в Sозначает сходимость почти всюду. Все пространства Lp=[0,1], р>0, являются l-идеалами в S, ипотому они тоже являются К.-п.
почти всюду для любого п), то функция x(t) = sup xn(t).и будет верхней гранью множества А, т. е. sup Авычисляется поточечно. Однако для несчетных множеств вычисление граней таким же способом уже невозможно, и существование у несчетных множеств ограниченных множеств в Sустанавливается сложнее, (о)-сходимость в Sозначает сходимость почти всюду. Все пространства Lp=[0,1], р>0, являются l-идеалами в S, ипотому они тоже являются К.-п.
Важную роль играет теорема Рисса - Канторовича о том, что множество всех порядково ограниченных операторов (т. <е. линейных операторов, переводящих ограниченные по упорядочению множества в такие же) из в. р. в К.-п. при естественном порядке (
 означает, что
означает, что  при всех
при всех  ) само является К.-п. Теория К.-п. нашла приложения в выпуклом анализе и теории экстремальных задач. Многие результаты здесь основываются на теореме Хана - Банаха - Канторовича о продолжении линейных операторов со значениями в К.-п.
) само является К.-п. Теория К.-п. нашла приложения в выпуклом анализе и теории экстремальных задач. Многие результаты здесь основываются на теореме Хана - Банаха - Канторовича о продолжении линейных операторов со значениями в К.-п.
К.-п. наз. расширенным, если всякое множество его попарно дизъюнктных элементов ограничено. В расширенном К.-п. всегда существует слабая единица. Для любого К.-п. Xсуществует единственное (с точностью до изоморфизма) расширенное К.-п. У, в к-рое Xпогружается как l-идеал, а полоса в Y, порожденная X, совпадает с Y. Такое У наз. максимальным расширением К. - п. Пространство S[0, 1] - максимальное расширение для всех пространств Lp[0,1]. Понятие расширенного К.-п. играет существенную роль во всей теории П. п., в частности при представлении К. п. с помощью функций.
С в. р. и К.-п. тесно связано понятие решеточно-нормированного пространства - векторного пространства, каждому элементу к-рого сопоставлена его обобщенная норма, являющаяся элементом фиксированной в. р. и удовлетворяющая обычным для нормы аксиомам, в к-рых знак неравенства понимается в смысле порядка в указанной в. р. Такие пространства используются в теории функциональных уравнений (теоремы существования; методы приближенного решения; метод Ньютона - Канторовича; монотонные процессы последовательных приближений и т. д.).
Топологические полуунорядоченные пространства. В функциональном анализе используются также у. в. п., в к-рых одновременно определена еще нек-рая топология, согласованная с порядком. Простейший и важнейший пример такого пространства - банахова решетка. Обобщением понятия банаховой решетки служит локально выпуклая решетка.
Важный класс банаховых К.-п. составляют КВ-пространства (КВ-п.), Канторовича - Банаха пространства. Так называется банахово К.-п., удовлетворяющее двум дополнительным условиям: 1)
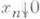 влечет
влечет  (порядковая непрерывность нормы); 2) если последовательность {х n} возрастает и не ограничена по порядку, то
(порядковая непрерывность нормы); 2) если последовательность {х n} возрастает и не ограничена по порядку, то  В КВ-п. удается описать с помощью нормы многие факты, опирающиеся по своему смыслу только на порядок.
В КВ-п. удается описать с помощью нормы многие факты, опирающиеся по своему смыслу только на порядок.
Напр.,
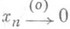 означает, что
означает, что  равномерно относительно т. Для того чтобы множество в КВ-п. Ебыло ограничено по порядку, необходимо и достаточно, чтобы ограниченным было множество всех чисел вида
равномерно относительно т. Для того чтобы множество в КВ-п. Ебыло ограничено по порядку, необходимо и достаточно, чтобы ограниченным было множество всех чисел вида  , где
, где  . КВ-п. есть регулярное К.-п.
. КВ-п. есть регулярное К.-п.
Пример КВ-п.: Lp[0,1] при
 .
.
Пусть X - произвольное локально выпуклое пространство, наделенное структурой у. в. п. и имеющее т. н. нормальный конус X+;при этом нормальность X+ равносильна тому, что в Xсуществует база окрестностей нуля, состоящая из абсолютно выпуклых и порядково насыщенных множеств U(последнее означает, что если
 и
и  , то и весь интервал [ х, у]
, то и весь интервал [ х, у]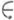 U). Для того чтобы каждый непрерывный линейный функционал на локально выпуклом у. в. п. был представим в виде разности положительных непрерывных линейных функционалов, необходима и достаточна нормальность конуса X+ в слабой топологии. Для нормированных пространств нормальность конуса в слабой и сильной топологии равносильны.
U). Для того чтобы каждый непрерывный линейный функционал на локально выпуклом у. в. п. был представим в виде разности положительных непрерывных линейных функционалов, необходима и достаточна нормальность конуса X+ в слабой топологии. Для нормированных пространств нормальность конуса в слабой и сильной топологии равносильны.
Лит.:[1] Вулих Б. 3., Введение в теорию полуупорядоченных пространств, М., 1961; [2] Канторович Л. В., Вулих Б. 3., Пинскер А. Г., Функциональный анализ в полуупорядоченных пространствах, М.- Л., 1950; [3] Шефер X., Топологические векторные пространства, пер. с англ., М., 1971; [4] Красносельский М. А., Положительные решения операторных уравнений, М., 1962; [5] Антоновский М. Я., Болтянский В. Г., Сарымсаков Т. А., Топологические алгебры Буля, Таш., 1963; [6] Биркгоф Г., Теория структур, пер. с англ., М., 1952; 17] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [8] Функциональный анализ, М., 1972 (Справоч. матем. б-ка); [9] Вулих Б. 3., Введение в теорию конусов в нормированных пространствах, Калинин, 1977; [10] Крейн М. Г., Рутман М. А., "Успехи матем. наук", 1948, т. 3, в. 1, с. 3-95; [11] Бухвалов А. В., Векслер А. И., Лозановский Г. Я., "Успехи матем. наук", 1979, т. 34. в. 2, с. 137-83; [12] Акилов Г. П., Кутателадзе С. С., Упорядоченные векторные пространства, Новосибирск, 1978. Б. 3. Вулих.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
