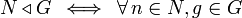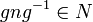Нормальный делитель

Нормальный делитель

В абстрактной алгебре нормальная подгруппа — это особый класс подгрупп, у которых левый и правый смежные классы совпадают. Они особенно важны потому, что позволяют строить факторгруппу по заданной группе.

Содержание

Определения

Подгруппа N группы G называется нормальной, если она инвариантна относительно сопряжений, то есть для любого элемента n из N и любого g из G, элемент gng − 1 лежит в N:

N \triangleleft G\, \iff\, \forall\, n\in N, g\in G \, gng^{-1}\in{N}

Следующие условия нормальности подгруппы эквивалентны:

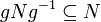  1. Для любого g из G, gNg^{-1} \sube N.
  2. Для любого g из G, gNg − 1 = N.
  3. Множества левых и правых смежных классов N в G совпадают.
  4. Для любого g из G, gN = Ng.

Условие (1) логически слабее, чем (2), а условие (3) логически слабее, чем (4). Поэтому условия (1) и (3) часто используются при доказательстве нормальности подгруппы, а условия (2) и (4) используются для доказательства следствий нормальности.

Примеры

  • {e} и G — всегда нормальные подгруппы G. Они называются тривиальными. Если других нормальных подгрупп нет, то группа G называется простой.
  • Все подгруппы N абелевой группы G нормальны, так как gN = Ng. Неабелева группа, у которой любая подгруппа нормальна, называется гамильтоновой.
  • Группа параллельных переносов в пространстве любой размерности — нормальная подгруппа евклидовой группы; например, в трёхмерном пространстве поворот, сдвиг и поворот в обратную сторону приводит к простому сдвигу.
  • В группе кубика Рубика, подгруппа, состоящая из операций, действующих только на угловые элементы, нормальна, так как никакое сопряжённое преобразование не заставит такую операцию действовать на краевой, а не угловой элемент. Напротив, подгруппа, состоящая лишь из поворотов верхней грани, не нормальна, так как сопряжения позволяют переместить части верхней грани вниз.

Свойства

  • Нормальность сохраняется при сюрьективных гомоморфизмах и взятии обратных образов.
  • Нормальность сохраняется при построении прямого произведения.
  • Нормальная подгруппа нормальной подгруппы не обязана быть нормальной в группе, то есть нормальность не транзитивна. Однако характеристическая подгруппа нормальной подгруппы нормальна.
  • Каждая подгруппа индекса 2 нормальна. Если p — наименьший простой делитель порядка G, то любая подгруппа индекса p нормальна.
  • Если N — нормальная подгруппа в G, то на множестве левых (правых) смежных классов G / N можно ввести групповую структуру по правилу
(g1N)(g2N) = (g1g2)N
Полученное множество называется факторгруппой G по N.
  • N нормальна тогда и только тогда, когда она тривиально действует на левых смежных классах G / N.

Исторические факты

Эварист Галуа первым понял важность нормальных подгрупп.

Ссылки

  • Винберг Э. Б. Курс алгебры — М.:Издательство «Факториал Пресс», 2002, ISBN 5-88688-060-7



Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "Нормальный делитель" в других словарях:

  • Нормальный делитель —         инвариантная подгруппа, одно из основных понятий теории групп (См. Группа), введённое Э. Галуа. Н. д. группы G подгруппа Н, для которой gH = Hg при любом выборе элемента g группы G …   Большая советская энциклопедия

  • НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ — нормальная подгруппа, инвариантная подгруппа, подгруппа Нгруппы G, для к рой левостороннее разложение группы Gпо подгруппе Нсовпадает с правосторонним, т. е. такая подгруппа, что для любого элемента смежные классы аН и На равны (в смысле… …   Математическая энциклопедия

  • Нормальный ряд подгрупп — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У …   Википедия

  • Нормальный ряд — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У …   Википедия

  • Глоссарий теории групп — Группа (математика) Теория групп …   Википедия

  • СИММЕТРИЧЕСКАЯ ГРУППА — группа всех подстановок (биекций) нек рого множества Xс операцией суперпозиции (см. Подстановок группа). С. г. подстановок множества Xобозначается S(X). Для равномощных Xи X группы S(X).и S (X ).подобны. В случае конечного множества X={1,2 …   Математическая энциклопедия

  • КОГОМОЛОГИЙ ГРУПП — исторически первая теория когомологий алгебр. Любой паре (G, А), где G группа, а А левый G модуль, т. е. модуль над целочисленным групповым кольцом Z(G), сопоставляется последовательность абелевых групп Hn(G, А), называемых группами когомологий… …   Математическая энциклопедия

  • КОМПАКТНАЯ ГРУППА — топологическая группа, компактная как топологич. пространство. Напр., всякая конечная группа (в дискретной топологии) является К. г. Алгебраическая группа, хотя она и является компактным топологич. пространством (относительно топологии Зариского) …   Математическая энциклопедия

  • ЛИ - КОЛЧИНА ТЕОРЕМА — разрешимая подгруппа Gгруппы GL(V)(V конечномерное векторное пространство над алгебраически замкнутым полем) имеет нормальный делитель G1 индекса не более где р зависит только от dim V, такой, что в Vсуществует флаг инвариантный относительно G1.… …   Математическая энциклопедия

  • ТОПОЛОГИЧЕСКАЯ ГРУППА — множество G, на к ром заданы две структуры группы и топологич. пространства, согласованные условием непрерывности групповых операций. А именно, отображение прямого произведения в G должно быть непрерывным. Подгруппа Н Т. г. Gявляется Т. г. в… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»