НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ

НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ

нормальная подгруппа, инвариантная подгруппа,- подгруппа Нгруппы G, для к-рой левостороннее разложение группы Gпо подгруппе Нсовпадает с правосторонним, т. е. такая подгруппа, что для любого элемента смежные классы аН и На равны (в смысле совпадения этих множеств). Если подгруппа Нявляется Н. д. группы G, то говорят также, что Ннормальна в G, и пишут . Если 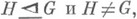то пишут . Подгруппа Ннормальна в группе Gтогда и только тогда, когда вместе с каждым своим элементом hона содержит все с ним сопряженные в группе G(см. Сопряженный элемент), т. е.. Н. д. может быть определен также как подгруппа, к-рая совпадает со всеми своими сопряженными подгруппами, вследствие чего он наз. также самосопряженной подгруппой.

При любом гомоморфизме 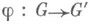множество Тэлементов группы G, отображающихся в единицу группы 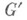(ядро гомоморфизма ), является Н. д. группы и обратно, всякий Н. д. группы Gесть ядро нек-рого гомоморфизма, в частности Н. д. Тслужит ядром канонич. гомоморфизма на факторгруппу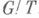

Пересечение любого множества Н. д., а также подгруппа, порожденная любой системой Н. д. группы G, Сами являются Н. д. группы G.

О. А. Иванова.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ" в других словарях:

  • Нормальный делитель — В абстрактной алгебре нормальная подгруппа  это особый класс подгрупп, у которых левый и правый смежные классы совпадают. Они особенно важны потому, что позволяют строить факторгруппу по заданной группе. Содержание 1 Определения 2 Примеры 3… …   Википедия

  • Нормальный делитель —         инвариантная подгруппа, одно из основных понятий теории групп (См. Группа), введённое Э. Галуа. Н. д. группы G подгруппа Н, для которой gH = Hg при любом выборе элемента g группы G …   Большая советская энциклопедия

  • Нормальный ряд подгрупп — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У …   Википедия

  • Нормальный ряд — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У …   Википедия

  • Глоссарий теории групп — Группа (математика) Теория групп …   Википедия

  • СИММЕТРИЧЕСКАЯ ГРУППА — группа всех подстановок (биекций) нек рого множества Xс операцией суперпозиции (см. Подстановок группа). С. г. подстановок множества Xобозначается S(X). Для равномощных Xи X группы S(X).и S (X ).подобны. В случае конечного множества X={1,2 …   Математическая энциклопедия

  • КОГОМОЛОГИЙ ГРУПП — исторически первая теория когомологий алгебр. Любой паре (G, А), где G группа, а А левый G модуль, т. е. модуль над целочисленным групповым кольцом Z(G), сопоставляется последовательность абелевых групп Hn(G, А), называемых группами когомологий… …   Математическая энциклопедия

  • КОМПАКТНАЯ ГРУППА — топологическая группа, компактная как топологич. пространство. Напр., всякая конечная группа (в дискретной топологии) является К. г. Алгебраическая группа, хотя она и является компактным топологич. пространством (относительно топологии Зариского) …   Математическая энциклопедия

  • ЛИ - КОЛЧИНА ТЕОРЕМА — разрешимая подгруппа Gгруппы GL(V)(V конечномерное векторное пространство над алгебраически замкнутым полем) имеет нормальный делитель G1 индекса не более где р зависит только от dim V, такой, что в Vсуществует флаг инвариантный относительно G1.… …   Математическая энциклопедия

  • ТОПОЛОГИЧЕСКАЯ ГРУППА — множество G, на к ром заданы две структуры группы и топологич. пространства, согласованные условием непрерывности групповых операций. А именно, отображение прямого произведения в G должно быть непрерывным. Подгруппа Н Т. г. Gявляется Т. г. в… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»