- Действие группы
-
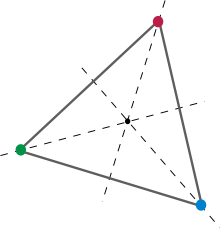 Вращения на углы кратные 120° вокруг центра равностороннего треугольника действует на множестве вершин этого треугольника, циклически переставляя их.
Вращения на углы кратные 120° вокруг центра равностороннего треугольника действует на множестве вершин этого треугольника, циклически переставляя их.
Действие группы на некотором множестве объектов позволяет изучать симметрии этих объектов с помощью аппарата теории групп.
Содержание
Определения
Действие слева
Говорят, что группа
 действует слева на множестве
действует слева на множестве  , если задан гомоморфизм
, если задан гомоморфизм  из группы
из группы  в симметрическую группу
в симметрическую группу  множества
множества  . Для краткости
. Для краткости  часто записывают как
часто записывают как  ,
,  или
или  . Элементы группы
. Элементы группы  называются в этом случае преобразованиями, а сама группа
называются в этом случае преобразованиями, а сама группа  — группой преобразований множества
— группой преобразований множества  .
.Другими словами, группа
 действует на множестве
действует на множестве  , если задано отображение
, если задано отображение  . обозначаемое
. обозначаемое  , такое что
, такое что для всех
для всех  ,
,  и
и , где
, где  — нейтральный элемент группы
— нейтральный элемент группы  . Можно сказать, что единица группы соотносит каждому элементу
. Можно сказать, что единица группы соотносит каждому элементу  его же; такое преобразование называется тождественным.
его же; такое преобразование называется тождественным.
Действие справа
Аналогично, правое действие группы
 на
на  задается гомоморфизмом
задается гомоморфизмом  , где
, где  — инверсная группа группы
— инверсная группа группы  . При этом часто используют сокращенное обозначение:
. При этом часто используют сокращенное обозначение:  . При этом аксиомы гомоморфизма записываются следующим образом:
. При этом аксиомы гомоморфизма записываются следующим образом:Комментарии
- Любое правое действие группы
 — это левое действие группы
— это левое действие группы  . Также, так как каждая группа изоморфна своей инверсной группе (изоморфизмом является, например, отображение
. Также, так как каждая группа изоморфна своей инверсной группе (изоморфизмом является, например, отображение  ), то из каждого правого действия можно с помощью такого изоморфизма получить левое действие. Поэтому, как правило, исследуются только левые действия.
), то из каждого правого действия можно с помощью такого изоморфизма получить левое действие. Поэтому, как правило, исследуются только левые действия.
- Если множество
 снабжено какой-то дополнительной структурой, то обычно предполагается, что отображение
снабжено какой-то дополнительной структурой, то обычно предполагается, что отображение  сохраняет эту структуру.
сохраняет эту структуру.
- Например, если
 — топологическое пространство, то
— топологическое пространство, то  предполагается непрерывным (а, значит, автоморфизмом). Такое действие более точно называется непрерывным действием.
предполагается непрерывным (а, значит, автоморфизмом). Такое действие более точно называется непрерывным действием.
- Например, если
Типы действий
- Свободное, если для любых различных
 и любого
и любого  выполняется
выполняется  .
. - Транзитивное если для любых
 существует
существует  такой, что
такой, что  . Другими словами, действие транзитивно, если
. Другими словами, действие транзитивно, если  для любого элемента
для любого элемента  .
. - Эффективное, если для любых
 существует
существует  такой, что
такой, что  .
. - Вполне разрывное, если для любого компактного множества
 , множество всех
, множество всех  , для которых пересечение
, для которых пересечение  непусто, конечно.
непусто, конечно.
На топологических пространствах и гладких многообразиях также особо рассматривают действия групп, наделенных соответствующими дополнительными структурами: топологических групп и групп Ли. Действие
 топологической группы на топологическом пространстве называют непрерывным, если оно непрерывно как отображение двух топологических пространств. Аналогично определяется гладкое действие группы Ли на гладком многообразии.
топологической группы на топологическом пространстве называют непрерывным, если оно непрерывно как отображение двух топологических пространств. Аналогично определяется гладкое действие группы Ли на гладком многообразии.- Непрерывное действие группы на пространстве жёстко (или квазианалитично), если из того, что некоторый элемент группы действует как тождественное отображение на некотором открытом множестве пространства, следует, что это единичный элемент группы.
- Любое эффективное непрерывное действие изометриями на связном римановом многообразии обязательно жёстко, чего нельзя сказать об общих метрических пространствах. Например, действие циклической группы порядка 2 перестановкой двух рёбер на графе, образованном тремя рёбрами, выходящими из одной точки, является эффективным, но не жёстким.
Орбиты
Подмножество
называется орбитой элемента
 .
.Действие группы
 на множестве
на множестве  определяет на нём отношение эквивалентности
определяет на нём отношение эквивалентностиПри этом классами эквивалентности являются орбиты элементов. Поэтому, если общее число классов эквивалентности равно
 , то
, тогде
 попарно неэквивалентны. Для транзитивного действия
попарно неэквивалентны. Для транзитивного действия  .
.Стабилизаторы
Подмножество
является подгруппой группы
 и называется стабилизатором или стационарной подгруппой элемента
и называется стабилизатором или стационарной подгруппой элемента  .
.Стабилизаторы элементов одной орбиты сопряжены, то есть если
 , то найдется такой элемент
, то найдется такой элемент  , что
, чтоКоличество элементов в орбите
![|Gm|=[G:G_m]](265fc0bedc4c8a3f94a78045ab819e07.png) ,
,  — стабилизатор элемента
— стабилизатор элемента  и
и ![[G:G_m]](722180d1b64ff27d70decdcf56ec6af2.png) — индекс подгруппы
— индекс подгруппы  , в случае конечных групп равен
, в случае конечных групп равен  .
.
Если
 , то
, то![|M|=\sum_{t=1}^k[G:G_{m_t}]](7b0b7485d9cdbeb3585bdba4cb3017e4.png) — формула разложения на орбиты.
— формула разложения на орбиты.
Эта формула также влечёт следующие тождества:
Примеры действий
Действия на себе
Слева
Действие на себе слева является наиболее простым примером действия, в этом случае,
 и гомоморфизм
и гомоморфизм  задан как
задан как  .
.Справа
Аналогично определяется действие на себе справа,
 .
.Слева и справа
Эти два действия являются действиями подгрупп прямого произведения
 на
на  с гомоморфизмом
с гомоморфизмом  заданым как
заданым как  .
.Сопряжениями
Пусть
 и гомоморфизм
и гомоморфизм  задан как
задан как  . При этом для каждого элемента
. При этом для каждого элемента  стабилизатор
стабилизатор  совпадает с централизатором
совпадает с централизатором  :
:Например, для элемента
 из центра группы
из центра группы  (то есть
(то есть  ) имеем
) имеем  и
и  .
.Вариации и обобщения
См. также
Литература
- Винберг, Э. Б. Курс алгебры. — 3-е изд. — М.: Издательство «Факториал Пресс», 2002. — ISBN 5-88688-0607.
- Кострикин, А. И. Введение в алгебру. Часть III. Основные структуры. — 3-е изд. — М.: ФИЗМАТЛИТ, 2004. — 272 с. — ISBN 5-9221-0489-6.
Категория:- Теория групп
Wikimedia Foundation. 2010.










