КОГОМОЛОГИЙ ГРУПП

- исторически первая теория когомологий алгебр.

Любой паре (G, А), где G- группа, а А - левый G-модуль, т. е. модуль над целочисленным групповым кольцом Z(G), сопоставляется последовательность абелевых групп Hⁿ(G, А), называемых группами когомологий группы Gс коэффициентами в А. Число п, пробегающее все целые неотрицательные значения, наз. размерностью группы Hⁿ(G, А). Группы К. г. являются важными инвариантами, содержащими информацию как о группе G, так и о модуле А.

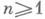Группа H⁰(G, А )равна, по определению, Ноm_G(Z, А)А ^G, где А ^G - подмодуль G-инвариантных элементов в А. Группы Hⁿ(G, А )для определяются как значения n-го производного функтора от функтора 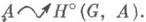Пусть

- некоторая проективная резольвента тривиального G-модуля Zв категории G-модулей, т. е. точная последовательность, в которой все модули Р, проективны. Тогда Hⁿ(G, A)- это n-я группа когомологий комплекса

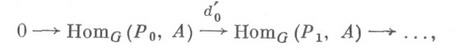
где отображения d'_n индуцированы отображениями d_rl, т. <е. Hⁿ(G, А) = Кеr d'_n/Im d'_n-1.

Группы гомологии групп определяются при помощи двойственной конструкции с заменой всюду функтора Hom_G функтором

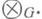
Набор функторов является когомологическим функтором (см. Гомологический функтор )на категории левых G-модулей.

Модуль вида В = Нот(Z [G], X), где X- абелева группа, a Gдействует на Впо формуле

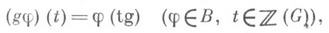
наз. коиндуцированным. Для инъективных и коиндуцированных модулей A Hⁿ(G, A) = 0 при Любой модуль Аизоморфен подмодулю нек-рого коиндуцированного модуля В. Точная когомологическая последовательность для последовательности определяет изоморфизмы 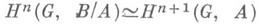и точную последовательность .

Таким образом, вычисление n+1-мерной группы когомологий для модуля Асводится к вычислению n-мерной группы когомологий для модуля В/А. Этот прием наз. сдвигом размерностей.

Сдвиг размерностей позволяет дать аксиоматическое определение групп когомологий, а именно, их можно определить как последовательность функторов 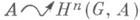из категории G-модулей в категорию абелевых групп, образующую когомологический функтор и удовлетворяющую условию Hⁿ(G, B) = 0 при для любого коиндуцированного модуля В.

Группы Hⁿ(G, А )можно определить также как классы эквивалентности точных последовательностей G-модулей вида

относительно подходящим образом определенной эквивалентности (см. [1], гл. 3, 4).

Для вычисления групп когомологий обычно используют стандартную резольвенту тривиального G-модуля Z, в которой Р _п=Z[G^{n + 1}]и для

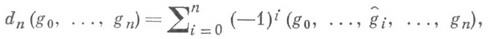
где знак означает, что член g_i опущен. Коцепи из Ноm_G( Р _n, А)- это функции f(g₀,..., g_n )такие, что gf(g₀, ..., g_n)=f(gg₀, ..., gg_n). Делая замену переменных по формулам g₀=1, g₁=h₁, g₂=h₁h₂, g_n=h₁h₂ ...h_n, можно перейти к неоднородным коцепям f(h₁, ..., h_n). Действие кограничного оператора на них таково: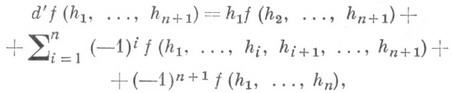

напр., одномерный коцикл - это функция f : такая, что f(g_lg₂) = g₁f(g₂)+f(g₁). для 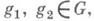а кограница - функция вида f(g) = ga -адля нек-рого Одномерный коцикл наз. также скрещенным гомоморфизмом, а одномерная коцепь - тривиальным скрещенным гомоморфизмом. В случае, когда G действует на Атривиально, скрещенные гомоморфизмы совпадают с обычными гомоморфизмами, а все тривиальные скрещенные гомоморфизмы равны 0, т. е. в этом случае H¹(G, A)=Hom (G, А).

Элементы группы H¹(G, А). можно интерпретировать как классы автоморфизмов группы F, содержащейся в точной последовательности 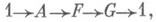тождественные на Аи на G по модулю сопряжений элементами Элементы группы Н ²(G, А) интерпретируются как классы расширений группы Ас помощью G. Наконец, группа H³(G, А )допускает интерпретацию в качестве препятствий для расширений неабелевой группы Нс центром Ас помощью G (см. [1]). Для n>3 аналогичная интерпретация групп Hⁿ(G, А )неизвестна (1978).

Если Н- подгруппа группы G, то ограничение коциклов с G на Нопределяет для всех пфункториальные гомоморфизмы ограничения

При n=0 res совпадает с вложением Если G/H- некоторая факторгруппа группы G, то подъем коциклов с G/H на G индуцирует функториальные гомоморфизмы инфляции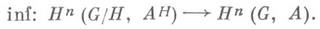

Пусть 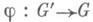- некоторый гомоморфизм. Тогда любой G-модуль Аможно превратить в G'-модуль, полагая для g' a=j(g')a. Комбинируя отображения res и inf, получают отображения Hⁿ(G, A) Hⁿ(G', А). В этом смысле H->(G, А )является контравариантным функтором по G. Если П - некоторая группа автоморфизмов группы G, то группы Hⁿ(G, A )можно превратить в П-модули. Напр., если Н- нормальный делитель в G, то группы Н ^п( Н, А )можно снабдить естественной структурой G/H-модулей. Это возможно благодаря тому, что внутренние автоморфизмы группы G индуцируют тождественные отображения на группах Hⁿ(G, А). В частности, для нормального делителя

Пусть Н- подгруппа группы G конечного индекса. Тогда отображение нормы позволяет, при помощи сдвига размерностей, определить для всех пфункториальные гомоморфизмы коограничения

удовлетворяющие соотношению cores-res= (G : Н).

Если Н- нормальный делитель в G, то существует спектральная последовательность Линдона, со вторым членом сходящаяся к когомологиям 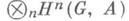(см. [1], гл. 2). В малых размерностях она приводит к точной последовательности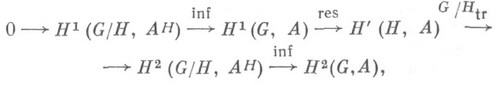

где tr - отображение трансгрессии.

Для конечной группы G норменное отображение N_G: индуцирует отображение 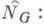H₀(G, A)H⁰(G, А), где H₀(G, A)-=A/J_GA и J_G- идеал кольца %(G), порожденный всеми элементами вида g-1 для Отображение Nq позволяет срастить точные последовательности когомологий и гомологии. Точнее, можно определить модифицированные группы когомологий - (называемые также когомологиям и Тейта) для всех целых п. При этом

Для этих когомологий существует точная бесконечная в обе стороны когомологическая последовательность. G-модуль А наз. когомологически тривиальным, если 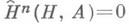для всех пи любой подгруппы 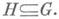Модуль Акогомологически тривиален тогда и только тогда, когда для нек-рого 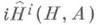=0 и 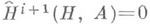для любой подгруппы НМ G.

Любой модуль Аможно представить как подмодуль или фактормодуль когомологически тривиального модуля, что позволяет применять сдвиг размерностей как для повышения, так и для понижения размерности. В частности, сдвиг размерностей позволяет определить отображения res и cores (но не inf) для всех целых п. Для конечно порожденного G-модуля Агруппы 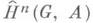конечны.

Группы аннулируются умножением на порядок G, а отображения индуцированные ограничениями, где G_p- некоторая силовская р-подгруппа группы G, мономорфны. Это позволяет сводить ряд вопросов о когомологиях конечных групп к рассмотрению когомологий р-групп. Когомологии циклической группы имеют период 2, т. е. для любого п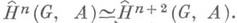

Для любых целых n и m определено отображение (наз. -произведением)

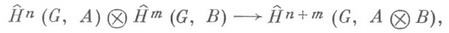
где тензорное произведение групп Аи Врассматривается как G-модуль. В частном случае, когда А- кольцо, и операции из группы Gявляются автоморфизмами, то -произведение превращает группу (G, А) в градуированное кольцо. Теорема двойственности для -произведения утверждает, что для любой полной абелевой группы Си G- модуля А 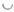-произведение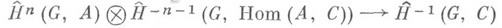

определяет изоморфизм между группами и 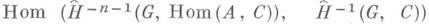(см. [2]).

-произведение определено и для бесконечной группы Gпри условии, что п, m>0.

Многие задачи приводят к необходимости рассмотрения когомологий топологич. группы G, непрерывно действующей на топологич. модуле А. В частности, если G- проконечная группа (случай наиболее близкий конечным группам) и А- дискретная абелева группа, являющаяся непрерывным G-модулем, то можно рассмотреть когомологии группы Gс коэффициентами в А, вычисляемые в терминах непрерывных коцепей [5]. Эти группы можно определить также как пределы lim Hⁿ(G/U, A^U )относительно отображений инфляции, где Uпробегает все открытые нормальные делители в G. Эти когомологии обладают всеми основными свойствами когомологий конечных групп. Если G- про-р-группа, то размерности над Z/pZ первой и второй групп ее когомологий с коэффициентами в z/pZ интерпретируются как минимальное число образующих и соотношений (между этими образующими) группы G.

О различных вариантах непрерывных когомологий, а также нек-рых других типах групп когомологий см. [6]. О К. г. с неабелевой группой коэффициентов см. Неабелевы когомологии.

Лит.:[1] Маклейн С, Гомология, пер. с англ., М., 1966; [2] Картан А., Эйленберг С, Гомологическая алгебра, пер. с англ., М., 1960; [3] Алгебраическая теория чисел, пер. с англ., М., 1969; [4] Серр Ж.-П., Когомологии Галуа, пер. с франц., М., 1968; [5] Кох X., Теория Галуа р-расширений, пер. с нем., М., 1973; [6] Итоги науки. Математика. Алгебра. 1964, М., 1966, с. 203-35.

Л. В. Кузьмин.