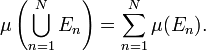Конечно аддитивная мера

Ме́ра — общее название различных типов обобщений понятий евклидовой длины, площади и n-мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно-аддитивная мера.

Определения

Конечно-аддитивная мера

Пусть задано пространство X с выделенным классом подмножеств 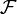$\mathcal{F}$, замкнутым относительно конечных пересечений и объединений.

Функция $\mu:\mathcal{F}\to[0,\;\infty]$ называется конечно-аддитивной мерой (иногда объёмом), если она удовлетворяет следующим аксиомам:

1. $\mu(\varnothing)=0$.
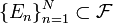2. Если $\{E_n\}_{n=1}^N\subset\mathcal{F}$ — конечное семейство попарно непересекающихся множеств из 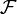$\mathcal{F}$, то есть 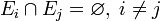$E_i\cap E_j=\varnothing,\;i\neq j$, то

$\mu\left(\bigcup\limits_{n=1}^N E_n\right)=\sum\limits_{n=1}^N\mu(E_n).$

Альтернативное определение

Система множеств σ называется полукольцом, если она содержит пустое множество, замкнута по отношению к образованию пересечений и обладает тем свойством, что из принадлежности к σ множества A и 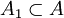$A_1\subset A$ вытекает возможность представления множества A в виде объединения 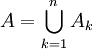$A=\bigcup_{k=1}^n A_k$, где A_k — попарно непересекающиеся множества из σ, первое из которых есть заданное множество A₁.

Функция множества μ(A) называется мерой, если:

• область определения σ_μ функции μ(A) есть полукольцо множеств;
• значения $\mu(A)\geqslant 0$;
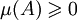• μ(A) — аддитивна, то есть для любого конечного разложения 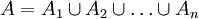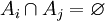$A=A_1\cup A_2\cup\ldots\cup A_n$, $A_i\cap A_j=\varnothing$ будет выполнено $\mu(A)=\sum_{k=1}^n\mu(A_k)$.

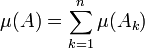Счётно-аддитивная мера

Пусть задано пространство X с выделенной σ-алгеброй $\mathcal{F}$.

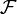Функция $\mu:\mathcal{F}\to[0,\;\infty]$ называется счётно-аддитивной (или σ-аддитивной) мерой, если она удовлетворяет следующим аксиомам:

1. $\mu(\varnothing)=0.$
2. (σ-аддитивность) Если 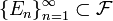$\{E_n\}_{n=1}^\infty\subset\mathcal{F}$ — счётное семейство попарно непересекающихся множеств из 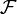$\mathcal{F}$, то есть 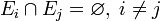$E_i\cap E_j=\varnothing,\;i\neq j$, то

$\mu\left(\bigcup\limits_{n=1}^\infty E_n\right)=\sum\limits_{n=1}^\infty\mu(E_n)$.

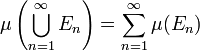Замечания

• Очевидно, любая счётно-аддитивная мера является конечно-аддитивной, но не наоборот.
• Если мера всего пространства конечна, то есть 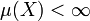$\mu(X)<\infty$, то такая мера сама по себе называется конечной. В противном случае мера бесконечна.
• На прямой и двумерной плоскости существует бесконечное число расширений лебеговой меры с σ-алгебры, порождаемой открытыми множествами, на множество всех подмножеств, сохраняющее конечную аддитивность меры. Ни для одного из нетривиальных евклидовых пространств не существует какого-либо счётно-аддитивного расширения лебеговой меры на множество всех его подмножеств.

Связанные определения

• Тройка 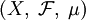$(X,\;\mathcal{F},\;\mu)$ называется пространством с мерой, если 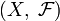$(X,\;\mathcal{F})$ есть измеримое пространство, а 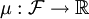$\mu:\mathcal{F}\to\R$ — определённая на нём мера.
• Если μ является вероятностной мерой, то такое пространство с мерой называется вероятностным пространством.

Примеры

• Мера Жордана — пример конечно-аддитивной меры.
• Мера Лебега — пример бесконечной меры.
• Вероятность — пример конечной меры.
• Мера Хаусдорфа
• Мера Бореля

Вариации и обобщения

• Заряд (теория меры)

Литература

• Вулих, Б. З. Краткий курс теории функций вещественной переменной (введение в теорию интеграла). — М.: Наука, 1973. — 352 с.