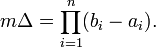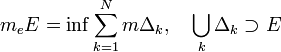Жорданова мера

Мера Жордана — один из способов формализации понятия длины, площади и n-мерного обьёма в n-мерном евклидовом пространстве.

Построение

Множество измеримо по Жордану если внутренняя мера Жордана равна внешней мере Жордана.

Мера Жордана mΔ параллелепипеда $\Delta=\prod_{i=1}^n [a_i,\;b_i]$ в $\R^n$ определяется как произведение

$m\Delta=\prod_{i=1}^n (b_i-a_i).$

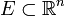Для ограниченного множества $E\subset\R^n$ определяются:

• внешняя мера Жордана

  $m_eE=\inf\sum_{k=1}^N m\Delta_k,\quad\bigcup_k\Delta_k\supset E$

• внутренняя мера Жордана

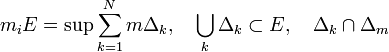  $m_iE=\sup\sum_{k=1}^N m\Delta_k,\quad\bigcup_k\Delta_k\subset E,\quad\Delta_k\cap\Delta_m$, если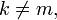 $k\neq m,$

здесь 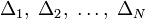$\Delta_1,\;\Delta_2,\;\ldots,\;\Delta_N$ — параллелепипеды описанного выше вида.

Множество E назывется измеримым по Жордану (квадрируемым при n = 2, кубируемым при 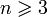$n\geqslant 3$), если m_eE = m_iE. В этом случае мера Жордана равна mE = m_eE = m_iE.

Свойства

• Мера Жордана инвариантна относительно движений евклидова пространства.
• Ограниченное множество 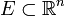$E\subset\R^n$ измеримо по Жордану тогда и только тогда, когда его граница имеет меру Жордана нуль (или, что равносильно, когда его граница имеет меру Лебега нуль).
• Внешняя мера Жордана одна и та же для E и 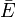$\bar E$ (замыкания множества E) и равна мере Бореля $\bar E$.
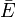• Измеримые по Жордану множества образуют кольцо множеств, на котором мера Жордана конечно аддитивная функция.

История

Приведённое понятие меры ввели Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Литература

• Peano, G. Applicazioni geometriche del calcolo infinitesimale. — Torino, 1887;
• Jordan, C. Journal de Mathématiques Pures et Appliquées. — 1892. — t. 8. — p. 69—99;

См. также

• Мера Лебега
• Мера множества
• Мера Хаусдорфа
• Мера Бореля