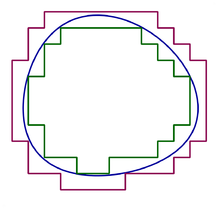
- Мера Жордана
-
Мера Жордана — один из способов формализации понятия длины, площади и
 -мерного объёма в
-мерного объёма в  -мерном евклидовом пространстве.
-мерном евклидовом пространстве.Содержание
Построение
Мера Жордана
 параллелепипеда
параллелепипеда ![\Delta=\prod_{i=1}^n [a_i,\;b_i]](e64e085278172bc3d72e230d41ae19b2.png) в
в  определяется как произведение
определяется как произведениеДля ограниченного множества
 определяются:
определяются:- внешняя мера Жордана
- внутренняя мера Жордана
 , если
, если 
здесь
 — параллелепипеды описанного выше вида.
— параллелепипеды описанного выше вида.Множество
 называется измеримым по Жордану (квадрируемым при
называется измеримым по Жордану (квадрируемым при  , кубируемым при
, кубируемым при  ), если
), если  . В этом случае мера Жордана равна
. В этом случае мера Жордана равна  .
.Свойства
- Мера Жордана инвариантна относительно движений евклидова пространства.
- Ограниченное множество
 измеримо по Жордану тогда и только тогда, когда его граница имеет меру Жордана нуль (или, что равносильно, когда его граница имеет меру Лебега нуль).
измеримо по Жордану тогда и только тогда, когда его граница имеет меру Жордана нуль (или, что равносильно, когда его граница имеет меру Лебега нуль).
- В частности, все множества, граница которых состоит из конечного числа гладких кривых и точек, измеримы по Жордану. Тем не менее, существуют множества, ограниченные простой замкнутой кривой Жордана, которые не измеримы по Жордану.
- Внешняя мера Жордана одна и та же для
 и
и  (замыкания множества
(замыкания множества  ) и равна мере Бореля
) и равна мере Бореля  .
. - Измеримые по Жордану множества образуют кольцо, на котором мера Жордана конечная аддитивная функция.
История
Приведённое понятие меры ввели Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Пример множества, неизмеримого по Жордану
Рассмотрим меру Жордана
 , определённую на
, определённую на  и пусть
и пусть  — множество точек единичного квадрата. Пусть
— множество точек единичного квадрата. Пусть  — множество, состоящее из всех точек множества
— множество, состоящее из всех точек множества  с рациональными координатами, тогда
с рациональными координатами, тогда  — неизмеримое по Жордану множество, так как
— неизмеримое по Жордану множество, так как  , то есть верхняя и нижняя мера Жордана не совпадают.
, то есть верхняя и нижняя мера Жордана не совпадают.Литература
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.
- Кудрявцев Л.Д., Кутасов А.Д. Сборник задач по математическому анализу, глава 2;
- Peano, G. Applicazioni geometriche del calcolo infinitesimale. — Torino, 1887;
- Jordan, C. Journal de Mathématiques Pures et Appliquées. — 1892. — t. 8. — p. 69—99;
См. также
- Мера множества
- Мера Лебега
- Мера Хаусдорфа
- Мера Бореля (англ.)
Категории:- Евклидова геометрия
- Теория меры
Wikimedia Foundation. 2010.