- МЕРА
мера множества,- обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек-ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в связи с изучением и усовершенствованием понятия интеграла.
Определения и общие свойства. Пусть X- нек-рое множество и
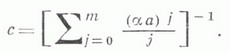 - нек-рый класс его подмножеств. Неотрицательная (не обязательно конечная) функция множеств
- нек-рый класс его подмножеств. Неотрицательная (не обязательно конечная) функция множеств 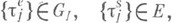 , определенная на
, определенная на 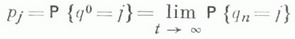 , наз. аддитивной, конечно аддитивной или счетно аддитивной, если
, наз. аддитивной, конечно аддитивной или счетно аддитивной, если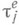
когда
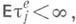
соответственно при п=2, п- любом конечном и

Совокупность
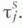 подмножеств множества Xназ. полукольцом множеств, если:
подмножеств множества Xназ. полукольцом множеств, если: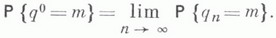
существует представление
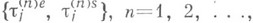 при
при 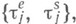 Совокупность
Совокупность  подмножеств множества Xназ. кольцом множеств, если:
подмножеств множества Xназ. кольцом множеств, если:
Пример полукольца:
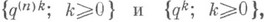 - совокупность интервалов вида
- совокупность интервалов вида
Совокупность всевозможных конечных объединений таких интервалов является кольцом.
Совокупность
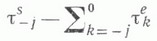 подмножеств множества Xназ. s -кольцом, если
подмножеств множества Xназ. s -кольцом, если
Всякое s-кольцо является кольцом; всякое кольцо является полукольцом.
Конечно аддитивной мерой наз. неотрицательная конечно аддитивная функция множеств ттакая, что
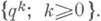 Областью определенияко
Областью определенияко 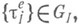 нечно аддитивной М. может быть полукольцо, кольцо или s-кольцо. В определении конечно аддитивной меры на кольце или s-кольце условие конечной аддитивности можно ослабить до аддитивности - при этом получается то же понятие.
нечно аддитивной М. может быть полукольцо, кольцо или s-кольцо. В определении конечно аддитивной меры на кольце или s-кольце условие конечной аддитивности можно ослабить до аддитивности - при этом получается то же понятие.Если т- конечно аддитивная М. множества Е,
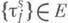 принадлежат области ее определения и
принадлежат области ее определения и то
то 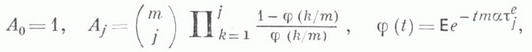
Конечно аддитивная М.
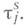 с областью определения
с областью определения  наз. продолжением конечно аддитивной меры М. т 1 с областью определения
наз. продолжением конечно аддитивной меры М. т 1 с областью определения 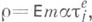 , если
, если 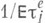
 . и
. и  при
при 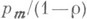 .
.Всякая конечно аддитивная М. т, определенная на полукольце
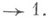 , может быть однозначно продолжена до конечно аддитивной М.
, может быть однозначно продолжена до конечно аддитивной М. 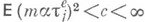 на наименьшем кольце
на наименьшем кольце  содержащем
содержащем 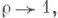 . Это продолжение определяется следующим образом: любое
. Это продолжение определяется следующим образом: любое 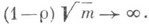 представимо в виде
представимо в виде 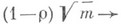 полагают равным
полагают равным 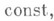
Конечно аддитивная М., обладающая свойством счетной аддитивности, наз. мерой. Пример меры: пусть Xпроизвольное непустое множестве,
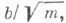 - о-кольцо, кольцо или полукольцо подмножеств X,
- о-кольцо, кольцо или полукольцо подмножеств X, 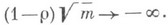 - счетное подмножество X,
- счетное подмножество X, - неотрицательные числа. Тогда функция
- неотрицательные числа. Тогда функция 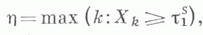 где
где  при
при 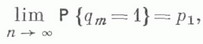 при
при  , является М., определенной на
, является М., определенной на  . Меры
. Меры 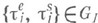 наз. элементарными, или вырожденными, мерами. Не всякая конечно аддитивная М. является М. Напр., если Xесть множество рациональных точек отрезка
наз. элементарными, или вырожденными, мерами. Не всякая конечно аддитивная М. является М. Напр., если Xесть множество рациональных точек отрезка 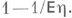 - полукольцо пересечений всевозможных подинтервалов
- полукольцо пересечений всевозможных подинтервалов  с Xи для любых
с Xи для любых 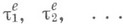

то
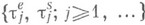 конечна, но не счетно аддитивна на
конечна, но не счетно аддитивна на  (Конечно аддитивная) М. тс областью определения
(Конечно аддитивная) М. тс областью определения 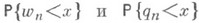 наз. конечной (соответственно s-конечной), если
наз. конечной (соответственно s-конечной), если 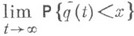 для любого
для любого 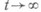 (соответственно, если для любого
(соответственно, если для любого 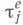 существует последовательность множеств
существует последовательность множеств  из
из 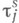 такая, что
такая, что 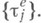
 ). (Конечно аддитивная) М. тназ. вполне конечной (вполне s-конечной), если она конечна (соответственно s-конечна) и
). (Конечно аддитивная) М. тназ. вполне конечной (вполне s-конечной), если она конечна (соответственно s-конечна) и 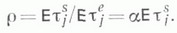 . Пара
. Пара 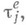 , где X- множество и
, где X- множество и 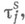 есть
есть  -кольцо
-кольцоего подмножеств такое, что
 , наз. измеримым пространством. Тройка
, наз. измеримым пространством. Тройка  , где
, где  - измеримое пространство и
- измеримое пространство и  есть М. на
есть М. на 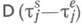 , наз. пространством с мерой. Пространство с вполне конечной М.
, наз. пространством с мерой. Пространство с вполне конечной М.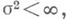 , нормированной условием
, нормированной условием  , наз. вероятностным пространством. В абстрактной теории М., где исходным является измеримое пространство
, наз. вероятностным пространством. В абстрактной теории М., где исходным является измеримое пространство  или пространство с М.
или пространство с М.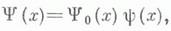 множества из
множества из  наз. измеримыми множествам и.
наз. измеримыми множествам и.Свойства пространства с мерой. Пусть
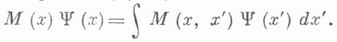 - произвольная последовательность измеримых множеств, тогда
- произвольная последовательность измеримых множеств, тогда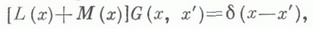
для нек-рого i0, то

3) если lim Ei существует и выполнено условие из 2), то

Определенная на кольце конечно аддитивная М. является М. тогда и только тогда, когда
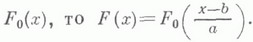
для любой монотонно возрастающей последовательности
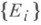 множеств из
множеств из 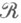 такой, что
такой, что 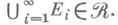
Пусть
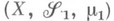 - пространство с М.,
- пространство с М., - измеримое пространство и Т-измеримое отображение
- измеримое пространство и Т-измеримое отображение 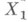 в
в  , т. е.
, т. е. 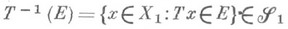 для любого
для любого  . Мерой, порожденной отображением Т(обозначается mT -1 ), наз. М. на
. Мерой, порожденной отображением Т(обозначается mT -1 ), наз. М. на  , определяемая соотношением ,
, определяемая соотношением , 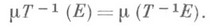
Пусть
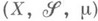 - измеримое пространство и
- измеримое пространство и  . Пусть на множествах
. Пусть на множествах  Е из s-кольца
Е из s-кольца 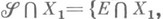
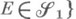
Тогда
 есть измеримое пространство; М.
есть измеримое пространство; М.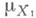 наз. ограничением меры
наз. ограничением меры  на
на 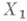 Атомом пространства с М.
Атомом пространства с М.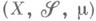 (или меры
(или меры  ) наз. всякое множество
) наз. всякое множество  положительной меры такое, что если
положительной меры такое, что если 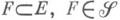 , то
, то  либо
либо 
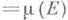 . Пространство с М., не содержащее атомов, наз. неатомическим, или непрерывным (сама М. при этом тоже наз. неатомической, или непрерывной). Если
. Пространство с М., не содержащее атомов, наз. неатомическим, или непрерывным (сама М. при этом тоже наз. неатомической, или непрерывной). Если  -пространство с неатомич.
-пространство с неатомич. -конечной М. и
-конечной М. и  то для любого
то для любого 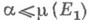 (возможно, равного
(возможно, равного  ) существует такой элемент
) существует такой элемент  , что
, что  и
и 
Пространство с М.
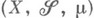 (или мера
(или мера 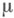 ) наз. полным, если из
) наз. полным, если из  следует, что
следует, что  . Всякое пространство с М.
. Всякое пространство с М.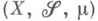 можно пополнить,
можно пополнить,если к
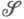 присоединить множества вида
присоединить множества вида  , где
, где 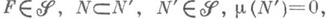 и положив для них
и положив для них  . Класс множеств указанного вида образует s-кольцо, при этом
. Класс множеств указанного вида образует s-кольцо, при этом 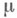 - полная М. на нем. Множества нулевой М. наз. нулевыми множествами. Если множество точек из X, для к-рых нек-рое свойство Qне выполняется, является нулевым множеством, то говорят, что свойство Qвыполняется почти всюду.
- полная М. на нем. Множества нулевой М. наз. нулевыми множествами. Если множество точек из X, для к-рых нек-рое свойство Qне выполняется, является нулевым множеством, то говорят, что свойство Qвыполняется почти всюду.Продолжение мер. М.
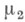 есть продолжение М.
есть продолжение М.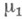 , если
, если 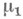 есть продолжение мер
есть продолжение мер 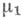 в классе конечно аддитивных М. (см. выше). Всякую определенную на полукольце
в классе конечно аддитивных М. (см. выше). Всякую определенную на полукольце  М. можно однозначно продолжить до М. на кольце
М. можно однозначно продолжить до М. на кольце 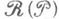 , порожденном
, порожденном  (продолжение осуществляется с помощью той же конструкции, что и в случае конечно аддитивных М.). Далее, всякую М.
(продолжение осуществляется с помощью той же конструкции, что и в случае конечно аддитивных М.). Далее, всякую М.  , определенную на кольце
, определенную на кольце  , можно продолжить до М.
, можно продолжить до М.  на порожденном
на порожденном 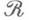
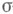 -кольцо
-кольцо 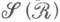 ; если
; если  s-конечна, то это продолжение единственно и s-конечно. Значение
s-конечна, то это продолжение единственно и s-конечно. Значение 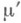 на множестве
на множестве 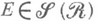 можно задать формулой
можно задать формулой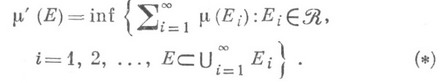
Наследственным классом подмножеств множества Xназ. всякий класс, содержащий вместе с каждым своим множеством любое его подмножество. Внешней мерой наз. функция множеств
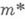 , определенная на наследственном s-кольце
, определенная на наследственном s-кольце  (классе множеств, являющемся одновременно наследственным классом и s-кольцом) и обладающая следующими свойствами:
(классе множеств, являющемся одновременно наследственным классом и s-кольцом) и обладающая следующими свойствами: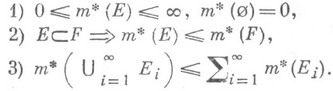
По М.
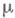 на кольце
на кольце 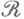 можно построить внешнюю М.
можно построить внешнюю М.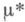 на наследственном s-кольце
на наследственном s-кольце 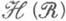 , порожденном
, порожденном  состоит из всех множеств, к-рые могут быть покрыты объединением счетного числа множеств из
состоит из всех множеств, к-рые могут быть покрыты объединением счетного числа множеств из 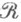 ), по формуле
), по формуле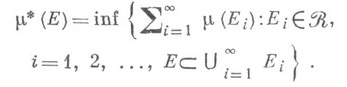
Внешняя М.
 наз. внешней мерой, индуцированной мерой
наз. внешней мерой, индуцированной мерой  Пусть
Пусть 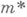 - внешняя М. на наследственном s-кольце
- внешняя М. на наследственном s-кольце 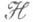 подмножеств X. Множество
подмножеств X. Множество  наз.
наз. 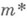 -измеримым, если
-измеримым, если
для любого
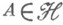 . Совокупность
. Совокупность  -измеримых множеств образует s-кольцо, содержащее все множества нулевой внешней М., а функция множеств
-измеримых множеств образует s-кольцо, содержащее все множества нулевой внешней М., а функция множеств  определяемая равенством
определяемая равенством 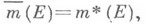 является полной мерой. М.
является полной мерой. М. наз. мерой, индуцированной внешней мерой
наз. мерой, индуцированной внешней мерой  .
.Пусть
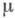 есть М. на кольце
есть М. на кольце 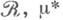 - внешняя М. на
- внешняя М. на 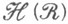 , индуцированная М.
, индуцированная М. 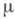 . Пусть
. Пусть 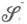 - совокупность
- совокупность 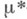 -измеримых множеств,
-измеримых множеств, 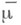 есть
есть  . на
. на 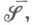 индуцированная внешней М.
индуцированная внешней М.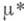 . Тогда М.
. Тогда М.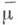 есть продолжение М.
есть продолжение М.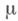 , и поскольку
, и поскольку 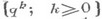 то функция
то функция  на
на  , задаваемая формулой (*), тоже М., продолжающая
, задаваемая формулой (*), тоже М., продолжающая  . Если исходная М.
. Если исходная М.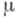 на
на 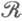 s-конечна, то пространство
s-конечна, то пространство 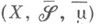 является пополнением пространства
является пополнением пространства  , см. (*). Если М.
, см. (*). Если М.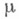 . задана на s -кольце
. задана на s -кольце 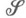 , то индуцированная ею внешняя М.
, то индуцированная ею внешняя М. на наследственном s-кольце
на наследственном s-кольце 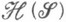 , порожденном
, порожденном  , дается формулой
, дается формулой
Наряду с внешней М.
 вводится понятие внутренней меры
вводится понятие внутренней меры 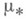 , индуцированной мерой
, индуцированной мерой  на
на 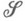 , именно:
, именно: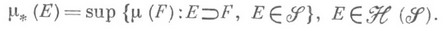
Для всякого множества
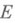 из
из  определяются его измеримое ядро
определяются его измеримое ядро 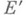 и измеримая оболочка
и измеримая оболочка 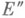 как множества из
как множества из  такие, что
такие, что  и
и  для любых
для любых 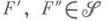 таких, что
таких, что  Измеримое ядро всегда существует, а измеримая оболочка существует всякий раз, когда
Измеримое ядро всегда существует, а измеримая оболочка существует всякий раз, когда  имеет s-конечную внешнюю М.; при этом
имеет s-конечную внешнюю М.; при этом 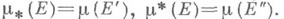 Пусть
Пусть  есть М. на кольце
есть М. на кольце  и
и 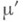 - ее продолжение на порожденное
- ее продолжение на порожденное 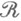
 кольцо
кольцо 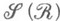 . Внутреннюю М.
. Внутреннюю М.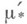 на подмножествах множества
на подмножествах множества 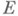 конечной
конечной  -меры можно выразить в терминах внешней М.
-меры можно выразить в терминах внешней М.  (а стало быть, и
(а стало быть, и 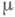 ):
):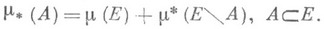
Кроме того, множество Fиз наследственного s-кольца
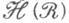 с конечной внешней
с конечной внешней 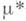 -мерой
-мерой 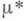 -измеримо тогда и только тогда, когда
-измеримо тогда и только тогда, когда  В случае, когда исходная М.
В случае, когда исходная М.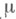 на
на 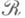 вполне конечна, справедливо следующее необходимое и достаточное условие
вполне конечна, справедливо следующее необходимое и достаточное условие 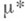 -измеримости множества
-измеримости множества 
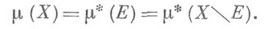
Для вполне конечных мер на
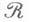 это условие нередко берется в качестве определения
это условие нередко берется в качестве определения  -измеримости Е.
-измеримости Е.Если
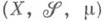 - измеримое пространство с
- измеримое пространство с 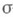 -конечной М. и
-конечной М. и  - конечное число множеств из наследственного s-кольца
- конечное число множеств из наследственного s-кольца 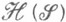 , порожденном
, порожденном 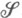 , то на s-кольце
, то на s-кольце  , порожденном
, порожденном 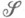 и множествами
и множествами  Х п , можно определить М.
Х п , можно определить М.  , совпадающую на
, совпадающую на  с
с  .
.Меры Жордана, Лебега и Лебега - Стилтьеса. Примером продолжения М. является мера Лебега в
 Интервалы вида
Интервалы вида 
образуют полукольцо
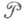 в
в 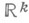 . Пусть для каждого такого интервала
. Пусть для каждого такого интервала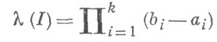
[
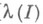 совпадает с объемом I]. Функция l
совпадает с объемом I]. Функция l 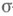 -конечна и счетно аддитивна на
-конечна и счетно аддитивна на  и однозначно продолжается до М. l' на s-кольце
и однозначно продолжается до М. l' на s-кольце 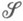 , порожденном
, порожденном  , к-рое совпадает с s-кольцом борелееских множеств (или множеств, измеримых по Борелю) в
, к-рое совпадает с s-кольцом борелееских множеств (или множеств, измеримых по Борелю) в 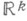 ; М.
; М. 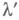 впервые была определена Э. Борелем (Е. Borel, 1898) (см. Бореля мера). Пополнение
впервые была определена Э. Борелем (Е. Borel, 1898) (см. Бореля мера). Пополнение 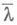 М. l' (определенное на
М. l' (определенное на 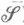 ) наз. мерой Лебега, введенной в 1902 А. Лебегом (Н. Lebesgue) (см. Лебега мера). Множества из области определения
) наз. мерой Лебега, введенной в 1902 А. Лебегом (Н. Lebesgue) (см. Лебега мера). Множества из области определения  меры
меры 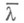 наз. измеримыми по Лебегу. Ограниченное множество
наз. измеримыми по Лебегу. Ограниченное множество 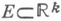 принадлежит
принадлежит  тогда и только тогда, когда
тогда и только тогда, когда 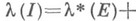
 , где
, где  -какой-либо интервал, содержащий Е, при этом
-какой-либо интервал, содержащий Е, при этом 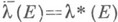 . Множество
. Множество  принадлежит
принадлежит 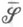 тогда и только тогда, когда
тогда и только тогда, когда  при всех пдля нек-рой последовательности {r п}, rn>0,
при всех пдля нек-рой последовательности {r п}, rn>0,  где
где  Мощность совокупности всех борелевских множеств в
Мощность совокупности всех борелевских множеств в 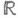 есть
есть 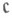 (мощность континуума), а мощность совокупности всех множеств, измеримых по Лебегу, есть
(мощность континуума), а мощность совокупности всех множеств, измеримых по Лебегу, есть  , так что включение
, так что включение  строгое, т. е. есть множества, измеримые по Лебегу и неизмеримые по Борелю.
строгое, т. е. есть множества, измеримые по Лебегу и неизмеримые по Борелю.Мера Лебега
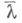 инвариантна относительно ортогональных линейных преобразований Апространства
инвариантна относительно ортогональных линейных преобразований Апространства  и относительно сдвигов на
и относительно сдвигов на 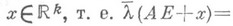
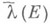 для любого
для любого 
Используя аксиому произвольного выбора, можно показать, что существуют множества, неизмеримые по Лебегу. Напр., на прямой таковым является множество, к-рое получится, если взять по одной точке из каждого класса смежности
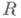 по аддитивной подгруппе рациональных чисел.
по аддитивной подгруппе рациональных чисел.Мерам Бореля и Лебега в
 исторически предшествовала М., определенная К. Жорданом (К. Jordan, 18921 (см. Жордана мера). Определение меры Жор-дана идейно весьма близко к классич. определению площади и объема, восходящему к древним грекам: множество
исторически предшествовала М., определенная К. Жорданом (К. Jordan, 18921 (см. Жордана мера). Определение меры Жор-дана идейно весьма близко к классич. определению площади и объема, восходящему к древним грекам: множество 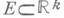 наз. измеримым по Жордану, если найдутся множества, являющиеся конечными объединениями непересекающихся прямоугольников, одно - содержащееся в Е, другое - содержащее Е, разность объемов (определяемых очевидным образом) к-рых сколь угодно мала. Мерой Жордана такого множества Еназ. нижняя грань объемов множеств - конечных объединений прямоугольников, накрывающих Е. Множество, измеримое по Жордану, измеримо и по Лебегу, и его мера Жордана совпадает с его мерой Лебега. Область определения меры Жордана является кольцом, но не s-кольцом, и это сильно сужает границы ее применимости.
наз. измеримым по Жордану, если найдутся множества, являющиеся конечными объединениями непересекающихся прямоугольников, одно - содержащееся в Е, другое - содержащее Е, разность объемов (определяемых очевидным образом) к-рых сколь угодно мала. Мерой Жордана такого множества Еназ. нижняя грань объемов множеств - конечных объединений прямоугольников, накрывающих Е. Множество, измеримое по Жордану, измеримо и по Лебегу, и его мера Жордана совпадает с его мерой Лебега. Область определения меры Жордана является кольцом, но не s-кольцом, и это сильно сужает границы ее применимости.Мера Лебега является частным случаем более общей меры Лебега - Стилтьеса. Последняя определяется посредством определенной на Rk действительной функции Fтакой, что
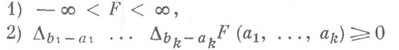
при
 где
где  - разностный оператор с шагом
- разностный оператор с шагом 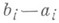 , взятый в точкеприменительно
, взятый в точкеприменительно 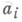
к i-й координате,

По заданной функции FМ.
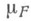 интервала
интервала
определяется формулой
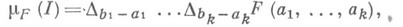
оказывается счетно аддитивной на полукольце всех таких интервалов и продолжается на s-алгебру борелевских множеств; пополнение этого продолжения и есть мера Лебега - Стилтьеса, отвечающая функции F. В частном случае, когда
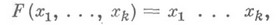
получается мера Лебега.
Меры в произведениях пространств. Произведением измеримых пространств
 и
и 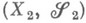 наз. измеримое пространство, образованное множеством
наз. измеримое пространство, образованное множеством  (произведением множеств
(произведением множеств 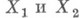 ) и s-кольцом
) и s-кольцом  его подмножеств (произведением s-колец
его подмножеств (произведением s-колец 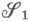 и
и 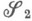 ), порожденным полукольцом
), порожденным полукольцом  множеств вида
множеств вида 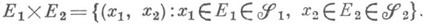
Если
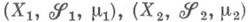 -пространства с М., то формула
-пространства с М., то формула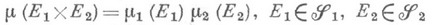
определяет М. на
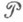 ; когда М.
; когда М.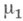 и
и  s-конечны, М. (д. однозначно продолжается до М. на
s-конечны, М. (д. однозначно продолжается до М. на 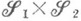 , обозначаемой
, обозначаемой 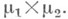 Мера
Мера  и пространство (
и пространство ( ,
, 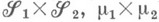 ) наз. соответственно произведением мер
) наз. соответственно произведением мер 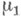 и
и 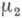 ипро изведен и ем пространств с мерой
ипро изведен и ем пространств с мерой  и
и 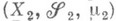 Пополнение произведения меры Лебега в
Пополнение произведения меры Лебега в 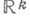 и меры Лебега в
и меры Лебега в 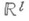 есть мера Лебега в
есть мера Лебега в 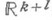 . Аналогично определяется произведение любого конечного числа пространств с М.
. Аналогично определяется произведение любого конечного числа пространств с М.Пусть
 - произвольная совокупность пространств с М. таких, что
- произвольная совокупность пространств с М. таких, что  Пространство-произведение
Пространство-произведение  по определению, есть множество всех функций на I, принимающих при каждом
по определению, есть множество всех функций на I, принимающих при каждом  значение
значение 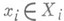 . Измеримым прямоугольником в Xназ. множество вида
. Измеримым прямоугольником в Xназ. множество вида  , где
, где  и лишь конечное число
и лишь конечное число  отлично от
отлично от 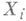 . Семейство измеримых прямоугольников образует полукольцо
. Семейство измеримых прямоугольников образует полукольцо  . Порожденное
. Порожденное 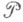 s-кольцо обозначается
s-кольцо обозначается 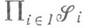 и наз. произведением s-колец
и наз. произведением s-колец  . Пусть
. Пусть  - функция на
- функция на  , определенная равенством
, определенная равенством 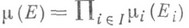 для
для  Так, определенная функция |х является М., к-рая может быть однозначно продолжена до М., обозначаемой
Так, определенная функция |х является М., к-рая может быть однозначно продолжена до М., обозначаемой  на
на  Пространство
Пространство 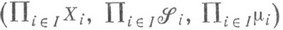 наз. произведением пространств
наз. произведением пространств 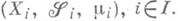
Произведение пространств с М. в произвольном числе является частным случаем следующей более общей схемы, играющей важную роль в теории вероятностей. Пусть
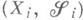 ,
,  ,- семейство измеримых пространств (
,- семейство измеримых пространств (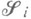 есть
есть  -алгебра) и пусть для каждого конечного множества
-алгебра) и пусть для каждого конечного множества  в измеримом пространство (
в измеримом пространство (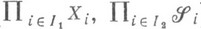 ) задана вероятностная М. mI , (произведение М. соответствует тому случаю, когда
) задана вероятностная М. mI , (произведение М. соответствует тому случаю, когда 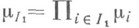 для любого конечного.
для любого конечного.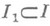 ). Пусть М.
). Пусть М. 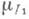 и
и  согласованы в том смысле, что если
согласованы в том смысле, что если  и
и 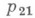 проекция
проекция 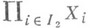 на
на 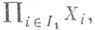 то
то  для вcех
для вcех  (по определинию,
(по определинию,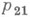 есть такое отображение
есть такое отображение  на
на 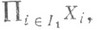 что
что 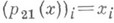 при всех
при всех 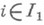 ). Существует ли вероятностная М. на
). Существует ли вероятностная М. на  такая, что для любого конечного
такая, что для любого конечного  и любого
и любого  справедливо равенство
справедливо равенство 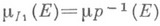 , где
, где  - проекция
- проекция  на
на 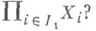 Оказывается, что такая М. существует не всегда, для ее существования нужны дополнительные условия. Одним из таких условий является совершенность М.
Оказывается, что такая М. существует не всегда, для ее существования нужны дополнительные условия. Одним из таких условий является совершенность М.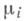 (отвечающих одноточечным множествам
(отвечающих одноточечным множествам  ). Понятие совершенной М. впервые было введено Б. В. Гнеденко и А. Н. Колмогоровым [6]. Пространство с вполне конечной М.
). Понятие совершенной М. впервые было введено Б. В. Гнеденко и А. Н. Колмогоровым [6]. Пространство с вполне конечной М.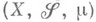 и сама М.
и сама М.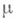 наз. совершенными, если для всякой
наз. совершенными, если для всякой  -измеримой действительной .функции
-измеримой действительной .функции 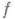 найдется такое борелевское множество
найдется такое борелевское множество 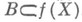 , что
, что 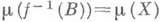 . В рамках совершенных М. невозможен целый ряд "патологических" явлений, возникающих в общей теории М.
. В рамках совершенных М. невозможен целый ряд "патологических" явлений, возникающих в общей теории М.Меры в топологических пространствах. При изучении М. в топологич. пространствах обычно рассматривают М., определенные на множествах, так или иначе связанных с топологией пространства. Один из типичных подходов состоит в следующем. Пусть X - произвольное топологич. пространство и
 - класс множеств вида f -1(F), где f - действительная непрерывная функция на Xи
- класс множеств вида f -1(F), где f - действительная непрерывная функция на Xи 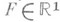 - замкнутое множество. Пусть
- замкнутое множество. Пусть 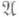 - алгебра, порожденная классом
- алгебра, порожденная классом 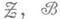 есть а-алгебра, порожденная
есть а-алгебра, порожденная 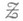 (
( наз. s-алгеброй бэровских множеств), и пусть
наз. s-алгеброй бэровских множеств), и пусть  - класс вполне конечных конечно аддитивных М. тна
- класс вполне конечных конечно аддитивных М. тна  , регулярных в том смысле, что
, регулярных в том смысле, что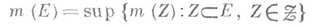
для любого
 . В
. В 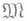 выделяют подмножества
выделяют подмножества  ,
, 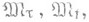 образованные (конечно аддитивными) М., обладающими дополнительными свойствами гладкости. По определению,
образованные (конечно аддитивными) М., обладающими дополнительными свойствами гладкости. По определению, для любой последовательности
для любой последовательности 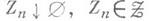 (это свойство равносильно счетной аддитивности m ;M. из
(это свойство равносильно счетной аддитивности m ;M. из  могут быть однозначно продолжены на
могут быть однозначно продолжены на 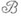 , и в дальнейшем они считаются заданными на
, и в дальнейшем они считаются заданными на  ),
), , если
, если  для любой сети
для любой сети 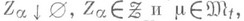 если для любого e>0
если для любого e>0 существует компакт Ктакой, что
существует компакт Ктакой, что 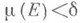 , когда Имеют место включения
, когда Имеют место включения  М. из Ms наз. бэровскими мерами.
М. из Ms наз. бэровскими мерами.Существует тесная связь между М. из
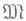 и линейными функционалами на пространстве С(X)ограниченных непрерывных функций на X. Именно, формула
и линейными функционалами на пространстве С(X)ограниченных непрерывных функций на X. Именно, формула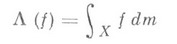
устанавливает взаимно однозначное соответствие между М.
 и неотрицательными линейными функционалами Л на С(X)(неотрицательность означает, что
и неотрицательными линейными функционалами Л на С(X)(неотрицательность означает, что  , когда
, когда 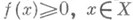 ). Более того, для любого
). Более того, для любого 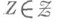
 где
где 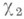 - индикатор множества Z. При этом М. из
- индикатор множества Z. При этом М. из  отвечают ст-гладкие функционалы
отвечают ст-гладкие функционалы 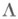 (т. <е. такие, что
(т. <е. такие, что  когда
когда 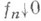 в С(Х)),М. из
в С(Х)),М. из  отвечают t - гладкие функционалы
отвечают t - гладкие функционалы 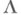 (т. <е. такие, что
(т. <е. такие, что  для любой сети
для любой сети 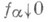 в
в  ) и М. из
) и М. из  соответствуют плотные функционалы Щ (т. е. такие, что
соответствуют плотные функционалы Щ (т. е. такие, что 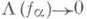 для любой сети
для любой сети  в С(Х)такой, что
в С(Х)такой, что 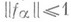 при всех
при всех 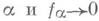 равномерно на компактных подмножествах; здесь
равномерно на компактных подмножествах; здесь 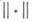 равномерная норма).
равномерная норма).В пространстве
 обычно рассматривается слабая топология
обычно рассматривается слабая топология 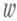 ; в этой топологии базисными окрестностями являются множества вида
; в этой топологии базисными окрестностями являются множества вида
В топологии
 есть вполне регулярное хаусдорфово пространство. Сходимость в топологии wобычно обозначается знаком =>. Для сходимости сети
есть вполне регулярное хаусдорфово пространство. Сходимость в топологии wобычно обозначается знаком =>. Для сходимости сети  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  и lim sup
и lim sup  для всех
для всех  . Другим необходимым и достаточным условием является
. Другим необходимым и достаточным условием является  для всех
для всех 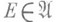 таких, что существует
таких, что существует 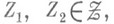 для к-рых
для к-рых 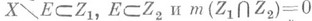 . Если пространство Xвполне регулярно и хаусдорфово, то
. Если пространство Xвполне регулярно и хаусдорфово, то 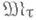 метризуемо тогда и только тогда, когда метризуомо X. Если X - метрич. пространство, то
метризуемо тогда и только тогда, когда метризуомо X. Если X - метрич. пространство, то  метризуемо как сепарабельное метрич. пространство тогда и только тогда, когда Xсепарабельно, и
метризуемо как сепарабельное метрич. пространство тогда и только тогда, когда Xсепарабельно, и 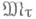 метризуемо как полное метрич. пространство тогда и только тогда, когда X метрпзуемо как полное метрич. пространство. Когда X метризуемо,
метризуемо как полное метрич. пространство тогда и только тогда, когда X метрпзуемо как полное метрич. пространство. Когда X метризуемо, 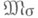 метризуемо тогда и только тогда, когда оно метризуемо Леви- Прохорова метрикой.
метризуемо тогда и только тогда, когда оно метризуемо Леви- Прохорова метрикой.Пространство
 секвенциально замкнуто в
секвенциально замкнуто в 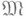 (теорема Александрова). Множество
(теорема Александрова). Множество  наз. плотным, если sup
наз. плотным, если sup и если для любого
и если для любого  существует компакт Ктакой, что
существует компакт Ктакой, что  , когда
, когда  ,
,  ,
,  . Если
. Если 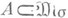 плотно, то Аотносительно компактно в
плотно, то Аотносительно компактно в  ; обратно, если X метризуемо и топологически полно,
; обратно, если X метризуемо и топологически полно, 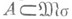 относительно компактно и каждая мера из Асосредоточена на нек-ром сепарабельном подмножестве, то Аплотно (теорема Прохорова).
относительно компактно и каждая мера из Асосредоточена на нек-ром сепарабельном подмножестве, то Аплотно (теорема Прохорова).При определенных условиях М. из
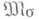 могут быть продолжены до борелевских М., т. е. М., определенных на s-алгебре борелевских множеств (см. Борелевское множество, Вореля мера). Так, если X - нормальное хаусдорфово счетно паракомпактное пространство, то каждая М.
могут быть продолжены до борелевских М., т. е. М., определенных на s-алгебре борелевских множеств (см. Борелевское множество, Вореля мера). Так, если X - нормальное хаусдорфово счетно паракомпактное пространство, то каждая М. может быть однозначно продолжена до регулярной борелевской М. Если X - вполне регулярно и хаусдорфово, то всякая t-гладкая (плотная) бзровская М. может быть однозначно продолжена до регулярной t-гладкой (плотной) борелевской М.
может быть однозначно продолжена до регулярной борелевской М. Если X - вполне регулярно и хаусдорфово, то всякая t-гладкая (плотная) бзровская М. может быть однозначно продолжена до регулярной t-гладкой (плотной) борелевской М.Носителем бэровской (борелевской) М. наз. наименьшое множество
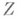 из
из 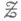 (наименьшее замкнутое множество), М. к-рого совпадает с М. всего пространства. У
(наименьшее замкнутое множество), М. к-рого совпадает с М. всего пространства. У  -гладких М. носители всегда существуют.
-гладких М. носители всегда существуют.Нередко при рассмотрении М. в топологич. пространствах (особенно-в локально компактных хаусдорфовых пространствах) борелевские и бэровские М. считают заданными на более узких классах множеств - на
 -кольцах, порожденных соответственно компактными множествами и компактными
-кольцах, порожденных соответственно компактными множествами и компактными 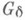 -множествами.
-множествами.Пусть G- локально компактная хаусдорфова топологич. группа. Левой мерой Хаарав Gназ. М., определенная на о-кольце, .порожденном всеми компактными множествами, не равная тождественно нулю и такая, что
 для любых
для любых 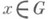 и Еиз области определения
и Еиз области определения 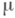 .Правая мера Хаара определяется аналогично заменой условия
.Правая мера Хаара определяется аналогично заменой условия  на условие
на условие  . В любой группе рассматриваемого типа существует и единственна (с точностью до мультипликативной положительной постоянной) левая мера Хаара. Всякая левая мера Хаара регулярна в том смысле, что
. В любой группе рассматриваемого типа существует и единственна (с точностью до мультипликативной положительной постоянной) левая мера Хаара. Всякая левая мера Хаара регулярна в том смысле, что  где К- компактные множества. Аналогичными свойствами обладает и правая мера Хаара., Мера Лебега в
где К- компактные множества. Аналогичными свойствами обладает и правая мера Хаара., Мера Лебега в  является частным случаем Хаара меры, См, также ст. Мера в топологическом векторном пространстве.
является частным случаем Хаара меры, См, также ст. Мера в топологическом векторном пространстве.Изоморфизм пространств с мерой. Пусть
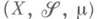 - пространство с М. Назовем множества
- пространство с М. Назовем множества 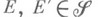 m - равными
m - равными  , если
, если  (здесь
(здесь 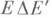 - симметрич. разность Еи Е'). Класс множеств
- симметрич. разность Еи Е'). Класс множеств 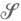 с таким определением равенства обозначим
с таким определением равенства обозначим 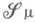 . В
. В 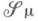 корректно определены теоретико-множественные операции, проводимые в конечном (или счетном) числе; напр., если
корректно определены теоретико-множественные операции, проводимые в конечном (или счетном) числе; напр., если 
 . Мера m. переносится очевидным образом на
. Мера m. переносится очевидным образом на 
Пусть
 -подмножество
-подмножество 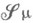 , состоящее из множеств конечной М. Функция
, состоящее из множеств конечной М. Функция  на
на  является метрикой. Пространство с М.
является метрикой. Пространство с М.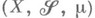 наз. сепарабельным, если
наз. сепарабельным, если 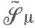 с метрикой
с метрикой 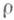 сепарабельно. Если
сепарабельно. Если  - пространство с s-конечной М. и s-кольцо
- пространство с s-конечной М. и s-кольцо  имеет счетное число образующих (т. е. существует счетное множество
имеет счетное число образующих (т. е. существует счетное множество 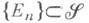 такое, что
такое, что  есть наименьшее содержащее его s-кольцо), то метрич. пространство
есть наименьшее содержащее его s-кольцо), то метрич. пространство  сепарабельно.
сепарабельно.Два пространства с М. (
 )и (
)и (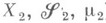 ) наз. изоморфными, если существует взаимно однозначное отображение
) наз. изоморфными, если существует взаимно однозначное отображение 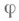 из
из 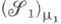 на
на  такое, что
такое, что  и
и  для любых
для любых 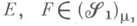 . Пусть теперь
. Пусть теперь  - произвольное пространство с вполне конечной М. Существует разбиение Xна непересекающиеся множества
- произвольное пространство с вполне конечной М. Существует разбиение Xна непересекающиеся множества 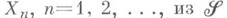 такое, что ограничение
такое, что ограничение  на
на 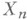 изоморфно либо М., сосредоточенной в одной точке, либо М., с точностью до положительного множителя равной прямому произведению
изоморфно либо М., сосредоточенной в одной точке, либо М., с точностью до положительного множителя равной прямому произведению где
где 
а множество
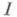 может иметь произвольную мощность (теорема Магарам - Колмогорова). Если пространство
может иметь произвольную мощность (теорема Магарам - Колмогорова). Если пространство  сепарабельно, неатомическое и
сепарабельно, неатомическое и 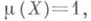 то оно изоморфно пространству
то оно изоморфно пространству  где
где 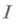 счетно, к-рое в свою очередь изоморфно единичному интервалу с мерой Лебега.
счетно, к-рое в свою очередь изоморфно единичному интервалу с мерой Лебега.Наряду с теорией М. как функции подмножеств нек-рого множества развита также теория М. как функции элементов булева кольца (или булевой алгебры);эти теории во многом параллельны. Другая распространенная конструкция М. восходит к У. Юнгу (W. Young) и П. Даниелю (P. Daniell) (см. [12]). Помимо теории положительных М., имеются также развитые теории М., значения к-рых действительны, комплексны или, вообще, принадлежат нек-рым алгебраич. структурам.
Лит.:[1] Сакс С, Теория интеграла, пер. с англ., М., 1949: [2] Xалмош П. Р., Теория меры, пер. с англ., М., 1953; [3] Данфорд Н., Шварц Дж ., Линейные операторы. Общая теория, пер. с англ., М., 1962; [4] Колмогоров А. Н., Фомин С. <В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [5] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969; [6] Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М.-Л., 1949; 17] Варадарайн В. С, "Матем. сб.", 1961, т. 55, № 1, с. 35-100; [8] Раrthasаrathу К. R., Probability measures on metric spaces, N. Y.-L., 1967;[9] Биллингсли П., Сходимость вероятностных мер, пер. с англ., М., 1977; [10] Сикорский Р., Булевы алгебры, пер. с англ., М., 1969; [11] Владимиров Д. А., Булевы алгебры, М., 1969; [12] Бурбаки Н., Интегрирование. Меры на локально компактных пространствах. Продолжение меры. Интегрирование мер. Меры на отделимых пространствах, пер. с франц., М., 1977; [13] Diestеl J., Uhl J., Vector measures, Providence, 1977.
В. В. Сазонов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
