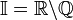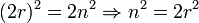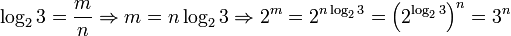Иррациональные числа

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби 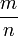$\frac{m}{n}$, где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа $\sqrt 2$.

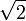Множество иррациональных чисел обычно обозначается 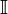$\mathbb I$. Таким образом

$\mathbb I =\R\backslash \Q$

— множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

Свойства

• Всякое вещественное число может быть записано бесконечной десятичной дробью, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
• Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
• Каждое трансцендентное число является иррациональным.
• Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
• Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
• Множество иррациональных чисел несчётно, является множеством второй категории.

Теоремы

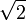$\sqrt{2}$ — иррациональное число

Допустим противное: 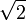$\sqrt{2}$ рационален, то есть представляется в виде несократимой дроби 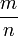$\frac{m}{n}$, где m и n — целые числа. Возведём предполагаемое равенство в квадрат:

$\sqrt{2} = \frac{m}{n} \Rightarrow 2 = \frac{m^2}{n^2} \Rightarrow m^2 = 2n^2$.

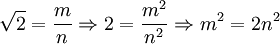Отсюда следует, что m² чётно, значит, чётно и m. Пускай m = 2r, где r целое. Тогда

$(2r)^2=2n^2 \Rightarrow n^2=2r^2$

Следовательно, n² чётно, значит, чётно и n. Мы получили, что m и n чётны, что противоречит несократимости дроби 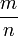$\frac{m}{n}$. Значит, исходное предположение было неверным, и 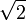$\sqrt{2}$ — иррациональное число.

log₂3 — иррациональное число

Допустим противное: log₂3 рационален, то есть представляется в виде дроби 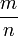$\frac{m}{n}$, где m и n — целые числа. Поскольку log₂3 > 0, m и n могут быть выбраны положительными. Тогда

$\log_2 3 = \frac{m}{n} \Rightarrow m = n \log_2 3 \Rightarrow 2^m = 2^{n \log_2 3} = \left (2^{\log_2 3}\right )^n = 3^n$

Но 2^m чётно, а 3ⁿ нечётно. Получаем противоречие.

e — иррациональное число

См. раздел «Доказательство иррациональности» в статье «e».

Другие иррациональные числа

Иррациональными являются:

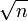• $\sqrt{n}$ для любого натурального n, не являющегося точным квадратом
• e^x для любого рационального $x\ne 0$
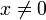
• lnx для любого положительного рационального $x\ne 1$
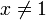
• π, а также πⁿ для любого натурального n

Числа

натуральные | целые | рациональные | вещественные | p-адические
иррациональные | алгебраические | трансцендентные
комплексные | дуальные | двойные
кватернионы | числа Кэли (октавы) | седенионы | гиперкомплексные