- Неравенство Йенсена
-
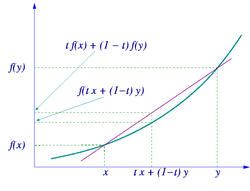
Нера́венство Йе́нсена — неравенство введённое Иоганом Йенсеном и тесно связанное с определением выпуклой функции.
Содержание
Формулировки
Конечный случай
Пусть функция
 является выпуклой на некотором промежутке
является выпуклой на некотором промежутке  и числа
и числа  таковы, что
таковы, что  и
и  . Тогда каковы бы ни были числа
. Тогда каковы бы ни были числа  из промежутка
из промежутка  , выполняется неравенство:
, выполняется неравенство:или
 .
.
Замечания:
- Если функция
 вогнута (выпукла вверх), то знак в неравенстве меняется на противоположный.
вогнута (выпукла вверх), то знак в неравенстве меняется на противоположный. - Сам Иоган Йенсен исходил из более частного соотношения, а именно
 , оно отвечает случаю
, оно отвечает случаю  .
.
ДоказательствоДоказательство проводится методом математической индукции.
- Для
 неравенство следует из определения выпуклой функции.
неравенство следует из определения выпуклой функции. - Допустим, что оно верно для какого-либо натурального числа
 , докажем, что оно верно и для
, докажем, что оно верно и для  , то есть
, то есть
 .
.
С этой целью, заменим слева сумму двух последних слагаемых
 одним слагаемым
одним слагаемым ;
;
это даст возможность воспользоваться неравенством для
 и установить, что выражение выше не превосходит суммы
и установить, что выражение выше не превосходит суммы .
.
Остается лишь применить к значению функции в последнем слагаемом неравенство для
 . Таким образом по методу математической индукции неравенство Йенсена полностью оправдано.
. Таким образом по методу математической индукции неравенство Йенсена полностью оправдано.Интегральная формулировка
Для выпуклой функции
 и интегрируемой функции
и интегрируемой функции  выполняется неравенство
выполняется неравенствоВероятностная формулировка
Пусть
 — вероятностное пространство, и
— вероятностное пространство, и  — определённая на нём случайная величина. Пусть также
— определённая на нём случайная величина. Пусть также  — выпуклая (вниз) борелевская функция. Тогда если
— выпуклая (вниз) борелевская функция. Тогда если  , то
, то![\varphi(\mathbb{E}[X]) \leqslant \mathbb{E}[\varphi(X)]](5334c06382fc8047a45e7d3d7570eba0.png) ,
,
где
![\mathbb{E}[\cdot]](604da0d00f7bea22b542f8a7cd0d78a7.png) означает математическое ожидание.
означает математическое ожидание.Неравенство Йенсена для условного математического ожидания
Пусть в дополнение к предположениям, перечисленным выше,
 — под-σ-алгебра событий. Тогда
— под-σ-алгебра событий. Тогда![\varphi(\mathbb{E}[X|\mathcal{G}]) \leqslant \mathbb{E}[\varphi(X)|\mathcal{G}]](3e3530e7138e88ac4e7783e6d437560b.png) ,
,
где
![\mathbb{E}[\cdot|\mathcal{G}]](4aa15876c37edd57d287a36030b50bca.png) обозначает условное математическое ожидание относительно σ-алгебры
обозначает условное математическое ожидание относительно σ-алгебры  .
.Частные случаи
Неравенство Гёльдера
- Пусть
 , где
, где 
 (выпуклая функция). Имеем
(выпуклая функция). Имеем
 ,
,  и
и 
Обозначим
 , где
, где  - произвольные положительные числа, тогда неравенство запишется в виде
- произвольные положительные числа, тогда неравенство запишется в виде .
.
Заменяя здесь
 на
на  и
и  на
на  , получаем известное неравенство Гёльдера:
, получаем известное неравенство Гёльдера: .
.
Неравенство Коши
- Пусть
 (вогнутая функция). Имеем
(вогнутая функция). Имеем
 , или
, или  , потенцируя получаем
, потенцируя получаем  .
.
В частности при
 получаем неравенство Коши (среднее геометрическое не превосходит среднего арифметического)
получаем неравенство Коши (среднее геометрическое не превосходит среднего арифметического)![\sqrt[n]{x_1 \ldots x_n}\le\frac{x_1+\ldots+x_n}{n}](d15dee8c0e0b069cd5a03e27e2559532.png) .
.
Неравенство между средним гармоническим и средним геометрическим
- Пусть
 (выпуклая функция). Имеем
(выпуклая функция). Имеем
 . Положив
. Положив  и потенцируя, получаем
и потенцируя, получаем (среднее гармоническое не превосходит среднего геометрического)
(среднее гармоническое не превосходит среднего геометрического)
Неравенство между средним гармоническим и средним арифметическим
- Пусть
 (выпуклая функция). Имеем
(выпуклая функция). Имеем 
В частности при
 получаем, что среднее гармоническое не превосходит среднего арифметического:
получаем, что среднее гармоническое не превосходит среднего арифметического:Физический смысл
Представим себе, что к ёлочной гирлянде прикреплены фонари разной массы. Провисающая гирлянда — выпуклая функция. Неравенство Йенсена гласит: центр тяжести фонарей всегда выше гирлянды.
В непрерывном случае: центр тяжести неоднородной гирлянды всегда выше самой гирлянды.
См. также
Литература
- Зорич В. А. Гл. V. Дифференциальное исчисление // Математический анализ. Часть I. — 6-е изд. — М.: МЦНМО, 2012. — С. 289—290. — 2000 экз. — ISBN 978-5-94057-892-5
- Фихтенгольц Г. М. Гл. IV. Исследование функций с помощью производных // Курс дифференциального и интегрального исчисления. — 8-е изд. — М.: ФИЗМАТЛИТ, 2001. — Т. 1. — С. 336—337. — 5000 экз. — ISBN 5-9221-0156-0
Категории:- Неравенства
- Математический анализ
- Теория вероятностей
Wikimedia Foundation. 2010.