- Условное матожидание
-
Усло́вное математи́ческое ожида́ние в теории вероятностей - это среднее значение случайной величины относительно условного распределения.
Содержание
Определения
Будем считать, что дано вероятностное пространство
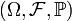 . Пусть
. Пусть 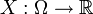 - интегрируемая случайная величина, то есть
- интегрируемая случайная величина, то есть 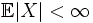 . Пусть также
. Пусть также 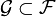 - под-σ-алгебра σ-алгебры
- под-σ-алгебра σ-алгебры 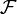 .
.УМО относительно σ-алгебры
Случайная величина
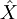 называется условным математическим ожиданием X относительно σ-алгебры
называется условным математическим ожиданием X относительно σ-алгебры 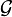 , если
, если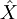 измерима относительно
измерима относительно 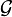 .
.![\forall A \in \mathcal{G},\quad \mathbb{E}\left[\hat{X} \mathbf{1}_A\right] = \mathbb{E}[X \mathbf{1}_A]](/pictures/wiki/files/99/cf22ef678a58fe160126bf26a91bf669.png) ,
,
где
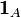 - индикатор события A. Условное математическое ожидание обозначается
- индикатор события A. Условное математическое ожидание обозначается ![\mathbb{E}[X \mid \mathcal{G}]](/pictures/wiki/files/100/d1324d3ae31593c374c4f1b8de5d80e6.png) .
.Пример. Пусть
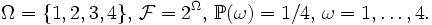 Положим
Положим 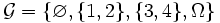 . Тогда
. Тогда 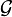 - σ-алгебра, и
- σ-алгебра, и 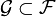 . Пусть случайная величина X имеет вид
. Пусть случайная величина X имеет вид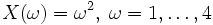 .
.
Тогда
УМО относительно семейства событий
Пусть
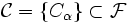 - произвольное семейство событий. Тогда условным математическим ожиданием X относительно
- произвольное семейство событий. Тогда условным математическим ожиданием X относительно 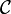 называется
называется![\mathbb{E}[X \mid \mathcal{C}] \equiv \mathbb{E}[X \mid \sigma(\mathcal{C})]](/pictures/wiki/files/57/98f747d6cf8c51d49f6446dda0d47f8d.png) ,
,
где
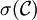 - минимальная сигма-алгебра, содержащая
- минимальная сигма-алгебра, содержащая 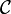 .
.Пример. Пусть
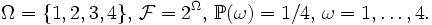 Пусть также C = {1,2,3}. Тогда
Пусть также C = {1,2,3}. Тогда 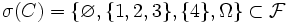 . Пусть случайная величина X имеет вид
. Пусть случайная величина X имеет вид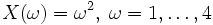 .
.
Тогда
УМО относительно случайной величины
Пусть
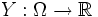 другая случайная величина. Тогда условным математическим ожиданием X относительно Y называется
другая случайная величина. Тогда условным математическим ожиданием X относительно Y называется![\mathbb{E}[X \mid Y] \equiv \mathbb{E}[X \mid \sigma(Y)]](/pictures/wiki/files/53/53641ebaf1d1ac60b0e8c0d971741d5f.png) ,
,
где σ(Y) - σ-алгебра, порождённая случайной величиной Y.
Другое определение УМО X относительно Y:
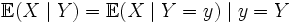
Такое определение конструктивно описывает алгоритм нахождения УМО:
- найти математическое ожидание случайной величины X, принимая Y за константу y;
- Затем в полученном выражении y обратно заменить на случайную величину Y.
Пример:
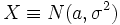
![\mathbb{E}\left[ \frac XY \mid Y \right] = \mathbb{E}\left[ \frac Xy \right] \mid_{y = Y} = \frac{1}{y}\mathbb{E}[ X ] \mid_{y = Y} = \frac{a}{y} \mid_{y = Y} = \frac{a}{Y}](/pictures/wiki/files/55/753dbecea424b90bca07854b7bf02fc2.png)
Условная вероятность
Пусть
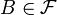 - произвольное событие, и
- произвольное событие, и 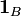 - его индикатор. Тогда условной вероятностью B относительно
- его индикатор. Тогда условной вероятностью B относительно 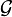 называется
называется![\mathbb{P}(B \mid \mathcal{G}) \equiv \mathbb{E}[\mathbf{1}_B \mid \mathcal{G}]](/pictures/wiki/files/102/f4638245b5423a630bd27953894bf4f5.png) .
.
Замечания
- Условное математическое ожидание - это случайная величина, а не число!
- Условное математическое ожидание определено с точностью до событий вероятности нуль. Таким образом, если
![\hat{X}_1 = \mathbb{E}[X \mid \mathcal{G}]](/pictures/wiki/files/49/1efa2d2e5fc4d688983fbe063f9293ff.png) и
и 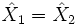
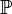 -почти всюду, то
-почти всюду, то ![\hat{X}_2 = \mathbb{E}[X \mid \mathcal{G}]](/pictures/wiki/files/49/1d0619660795edd16f0c29a87aa9f5e1.png) . Отождествив случайные величины, различающиеся лишь на событиях вероятности нуль, получаем единственность условного математического ожидания.
. Отождествив случайные величины, различающиеся лишь на событиях вероятности нуль, получаем единственность условного математического ожидания. - Взяв A = Ω, получаем по определению:
![\mathbb{E}[X] = \mathbb{E}[\mathbb{E}[X \mid \mathcal{G}]]](/pictures/wiki/files/56/81dffa5431ca56cb540ee16c2b1dea68.png) ,
,
и в частности справедлива формула полной вероятности:
![\mathbb{P}(B) = \mathbb{E}[\mathbb{P}(B\mid \mathcal{G})]](/pictures/wiki/files/51/3f59ad3ecb40356af526a29eb095c7e2.png) .
.
- Пусть σ-алгебра
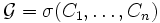 порождена разбиением
порождена разбиением 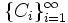 . Тогда
. Тогда
![\mathbb{E}[X \mid \mathcal{G}] = \sum_{i=1}^{\infty} \mathbb{E}[X \mid C_i] \mathbf{1}_{C_i}](/pictures/wiki/files/53/58bf7fc1dd87f31e37238b37201fb3e5.png) .
.
В частности формула полной вероятности принимает классический вид:
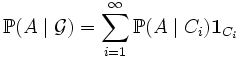 ,
,
а следовательно
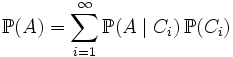 .
.
Основные свойства
- Если
![\hat{X} = \mathbb{E}[X \mid Y]](/pictures/wiki/files/54/6196d292b7b4fd682408d2a30efad640.png) , то существует борелевская функция
, то существует борелевская функция 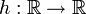 , такая что
, такая что
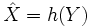 .
.
Условное математическое ожидание X относительно события {Y = y} по определению равно
![\mathbb{E}[X \mid Y = y] \equiv h(y)](/pictures/wiki/files/48/05e2b21fa206ab36460d71743f9ce32f.png) .
.
- Если
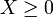 п.н., то
п.н., то ![\mathbb{E}[X \mid \mathcal{G}] \ge 0](/pictures/wiki/files/53/5d85ca57eca6e7a0367f1ea9ea53fc57.png) п.н.
п.н. - Если X независима от
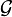 , то
, то
![\mathbb{E}[X \mid \mathcal{G}] = \mathbb{E}[X]](/pictures/wiki/files/101/e4f013d5ef95cd414b2f3108177bc25b.png) п.н.
п.н.
В частности, если X,Y независимые случайные величины, то
![\mathbb{E}[X \mid Y] = \mathbb{E}[X]](/pictures/wiki/files/102/f145bc2053544ebeb7cc85626c288d58.png) п.н.
п.н.
- Если
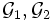 - две σ-алгебры, такие что
- две σ-алгебры, такие что 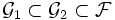 , то
, то
![\mathbb{E}[\mathbb{E}[X \mid \mathcal{G}_2]\mid \mathcal{G}_1] = \mathbb{E}[X \mid \mathcal{G}_1]](/pictures/wiki/files/98/b35bb195f79efcff0a853803bd9f4017.png) .
.
- Если X -
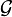 -измерима, и Y - случайная величина, такая что
-измерима, и Y - случайная величина, такая что 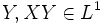 , то
, то
![\mathbb{E}[XY \mid \mathcal{G}] = X \, \mathbb{E}[Y \mid \mathcal{G}]](/pictures/wiki/files/56/86f481a9b3a571f3584847124368340c.png) .
.
- "Математическое ожидание убирает условие". Это правило верно для УМО относительно случайной величины (УМО в таком случае будет случайной величиной) и для условной вероятности относительно случайной величины
![\mathbb{E}[ \mathbb{E}(X \mid Y) ] = \mathbb{E}( X )](/pictures/wiki/files/57/99d587fce1db76ea28901b363678fefa.png) .
.
Дополнительные свойства
- Теорема Леви о монотонной сходимости;
- Теорема Лебега о мажорируемой сходимости;
- Лемма Фату;
- Неравенство Йенсена.
УМО для дискретных величин
Пусть Y - дискретная случайная величина, чьё распределение задаётся функцией вероятности
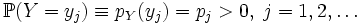 . Тогда система событий {Y = yj} является разбиением Ω, и
. Тогда система событий {Y = yj} является разбиением Ω, и![\mathbb{E}[X \mid Y] = \sum\limits_{j=1}^{\infty} \mathbb{E}[X \mid Y = y_j] \mathbf{1}_{\{Y = y_j\}}](/pictures/wiki/files/49/1dde031bb1f1e5d4387a889387f73fe6.png) ,
,
а
![\mathbb{E}[X \mid Y = y_j] = \mathbb{E}_{j}[X]](/pictures/wiki/files/51/3cfcfb1aa86a932d7defed477fc34fc3.png) ,
,
где
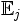 означает математическое ожидание, взятое относительно условной вероятности
означает математическое ожидание, взятое относительно условной вероятности 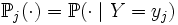 .
.Если случайная величина X также дискретна, то
![\mathbb{E}[X \mid Y = y_j] = \sum\limits_{i=1}^{\infty} x_i\, \mathbb{P}(X = x_i \mid Y = y_j) = \sum\limits_{i=1}^{\infty} x_i\, p_{X \mid Y}(x_i \mid y_j)](/pictures/wiki/files/51/3b070afd1b18ae3e0f699380994e77ef.png) ,
,
где
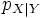 - условная функция вероятности случайной величины X относительно Y.
- условная функция вероятности случайной величины X относительно Y.УМО для абсолютно непрерывных случайных величин
Пусть X,Y - случайные величины, такие что вектор
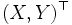 абсолютно непрерывен, и его распределение задаётся плотностью вероятности fX,Y(x,y). Введём условную плотность
абсолютно непрерывен, и его распределение задаётся плотностью вероятности fX,Y(x,y). Введём условную плотность 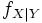 , положив по определению
, положив по определению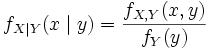 ,
,
где fY - плотность вероятности случайной величины Y. Тогда
![\mathbb{E}[X \mid Y] = h(Y)](/pictures/wiki/files/49/1f81518cc4d0097432950afa03407fb4.png) ,
,
где функция h имеет вид
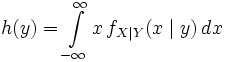 .
.
В частности,
![\mathbb{E}[X \mid Y = y_j] = \int\limits_{-\infty}^{\infty} x\, f_{X\mid Y}(x \mid y_j)\, dx](/pictures/wiki/files/101/ea0a686654b53c3375e61df821179770.png) .
.
УМО в L2
Рассмотрим пространство случайных величин с конечным вторым моментом L2. В нём определены скалярное произведение
![\langle X, Y\rangle \equiv \mathbb{E}[XY],\; \forall X,Y \in L^2](/pictures/wiki/files/100/dac5d5348398a5e725df4956adf42c68.png) ,
,
и порождённая им норма
![\|X\| = \sqrt{\mathbb{E}\left[X^2\right]},\; \forall X \in L^2](/pictures/wiki/files/54/6583b41b04c6518a0138d76c01afac08.png) .
.
Множество всех случайных величин
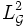 с конечным вторым моментом и измеримых относительно
с конечным вторым моментом и измеримых относительно 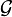 , где
, где 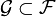 , является подпространством L2. Тогда оператор
, является подпространством L2. Тогда оператор 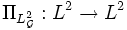 , задаваемый равенством
, задаваемый равенством![\Pi_{L^2_{\mathcal{G}}}(X) = \mathbb{E}[X \mid \mathcal{G}]](/pictures/wiki/files/52/4949d0a245dc92f16b1ffce57c8072ac.png) ,
,
является оператором ортогонального проектирования на
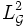 . В частности:
. В частности:- Условное математическое ожидание
![\mathbb{E}[X \mid \mathcal{G}]](/pictures/wiki/files/100/d1324d3ae31593c374c4f1b8de5d80e6.png) - это наилучшее средне-квадратичное приближение X
- это наилучшее средне-квадратичное приближение X 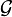 -измеримыми случайными величинами:
-измеримыми случайными величинами:
![\|X - \mathbb{E}[X\mid \mathcal{G}]\| = \inf\limits_{Z \in L^2_{\mathcal{G}}} \|X - Z\|](/pictures/wiki/files/98/bbc6b262800a6a417a6822183754bf64.png) .
.
- Условное математическое ожидание сохраняет скалярное произведение:
![\langle X, Z \rangle = \langle \mathbb{E}[X\mid \mathcal{G}] , Z\rangle,\; \forall Z \in L^2_{\mathcal{G}}](/pictures/wiki/files/48/0c117e471d5155bb1c88804533c4d983.png) .
.
- Условное математическое ожидание идемпотентно:
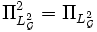 .
.
См. также
Wikimedia Foundation. 2010.

 = \left\{
\begin{matrix}
\frac{5}{2}, & \omega = 1,2 \\[5pt]
\frac{25}{2}, & \omega = 3,4.
\end{matrix}
\right.](/pictures/wiki/files/98/bc07cc947690098ee5fa25d523d72e49.png)
 = \left\{
\begin{matrix}
\frac{14}{3}, & \omega = 1,2,3 \\[5pt]
16, & \omega = 4.
\end{matrix}
\right.](/pictures/wiki/files/98/b121589cd23ec206a52f885d517d9ea4.png)