- Среднее геометрическое
-
Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально:
Среднее геометрическое двух чисел также называется их средним пропорциональным[1].
Содержание
Свойства
- Так же, как и любое другое среднее значение, с.г. лежит между минимумом и максимумом из всех чисел:
- Среднее геометрическое двух чисел
 является средним арифметическим-гармоническим этих чисел, то есть равно пределу двух последовательностей:
является средним арифметическим-гармоническим этих чисел, то есть равно пределу двух последовательностей:
- Среднее геометрическое двух чисел равно среднему геометрическому их среднего арифметического и среднего гармонического[2].
Среднее геометрическое взвешенное
Среднее геометрическое взвешенное набора вещественных чисел
 с вещественными весами
с вещественными весами  определяется как
определяется какВ том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому.
В геометрии
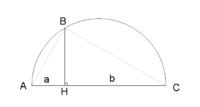
Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу, а каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
Это даёт геометрический способ построения среднего геометрического двух (длин) отрезков: нужно построить окружность на сумме этих двух отрезков как на диаметре, тогда высота, восставленная из точки их соединения до пересечения с окружностью, даст искомую величину.
Обобщения
- Среднее геометрическое можно рассматривать как предел средних степенных
![A_g(x_1,\ldots,x_n)=\sqrt[g]\frac{x_1^g+\ldots+x_n^g}{n}](7433412828a86e41d8b7767bb4e847dc.png) при
при  .
. - Среднее геометрическое является средним Колмогорова при

См. также
- Среднее арифметическое
- Среднее квадратическое
- Среднее значение
- Неравенство между средним арифметическим и средним геометрическим
- Неравенство Швейцера
Примечания
- ↑ «Среднее пропорциональное». — статья из Большой советской энциклопедии
- ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923.
Для улучшения этой статьи желательно?: - Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
Статистические показатели Описательная
статистикаНепрерывные
данныеКоэффициент сдвига Среднее (Арифметическое, Геометрическое, Гармоническое) · Медиана · Мода · Размах Вариация Ранг · Среднеквадратическое отклонение · Коэффициент вариации · Квантиль (Дециль, Процентиль/Перцентиль/Центиль) Моменты Математическое ожидание · Дисперсия · Асимметрия · Эксцесс Дискретные
данныеЧастота · Таблица контингентности Статистический
вывод и
проверка
гипотезСтатистический
выводДоверительный интервал (Частотная вероятность) · Достоверный интервал (Байесовский вывод) · Статистическая значимость · Мета-анализ Планирование
экспериментаГенеральная совокупность · Планирование выборки · Районированная выборка · Репликация · Группировка · Чувствительность и специфичность Объём выборки Статистическая мощность · Мера эффекта · Стандартная ошибка Общая оценка Байесовская оценка решения · Метод максимального правдоподобия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала Статистические
критерииZ-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Тест Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса Анализ выживания Функция выживания · Оценка Каплана — Мейера · Логранк-тест · Интенсивность отказов · Пропорциональная модель опасностей Корреляция Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания Линейные модели Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ Регрессия Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами Категория:- Средние величины
Wikimedia Foundation. 2010.

![G(x_1, x_2, \ldots, x_n)=\sqrt[n]{x_1x_2\cdots x_n}=\left(\prod_{i=1}^n x_i\right)^{1/n}](74108588886b9ca27511de02c9bd4a97.png)