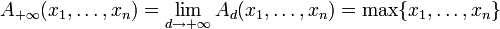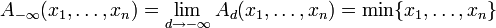- Неравенство о средних
-
Среднее степени d (или просто среднее степенное) набора положительных вещественных чисел
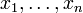 определяется как
определяется какПри этом по непрерывности доопределяются следующие величины:
Среднее степенное является частным случаем Колмогоровского среднего.
Содержание
Другие названия
Т.к. среднее степени d обобщает известные с древности (т.н. архимедовы) средние, то его часто называют средним обобщённым.
По связи с неравенствами Минковского и Гёльдера среднее степенное имеет также названия: среднее по Гёльдеру и среднее по Минковскому.
Частные случаи
Средние степеней 1, 0, −1 и 2 имеют собственные имена:
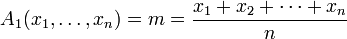 называется средним арифметическим;
называется средним арифметическим;
(иначе говоря: средним арифметическим n чисел является их сумма, деленная на n)
![A_0(x_1, \ldots, x_n) = g =\sqrt [n]{x_1 x_2\cdots x_n}](/pictures/wiki/files/101/e891fa8b215f0234778212e81509ee63.png) называется средним геометрическим;
называется средним геометрическим;
(иначе говоря: средним геометрическим n чисел является корень n-ой степени из произведения этих чисел)
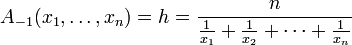 называется средним гармоническим.
называется средним гармоническим.
(иначе говоря: средним гармоническим чисел является обратная величина к среднему арифметическому их обратных)
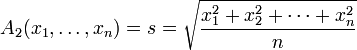 называется средним квадратичным (квадратическим), известным так же под сокращением RMS (root-mean-square).
называется средним квадратичным (квадратическим), известным так же под сокращением RMS (root-mean-square).
Соответственно (для наборов из положительных чисел)
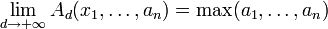 и
и 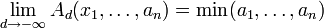
Неравенство о средних
Неравенство о средних утверждает, что для d1 > d2
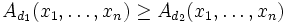 ,
,причем равенство достигается только в случае равенства всех аргументов
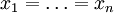 .
.Для доказательства неравенства о средних достаточно показать, что частная производная
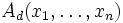 по d неотрицательна и обращается в ноль только при
по d неотрицательна и обращается в ноль только при 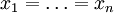 (например, используя неравенство Йенсена), и далее применить формулу конечных приращений.
(например, используя неравенство Йенсена), и далее применить формулу конечных приращений.Неравенство о среднем арифметическом, геометрическом и гармоническом
Частным случаем неравенства о средних является неравенство о среднем арифметическом, геометрическом и гармоническом
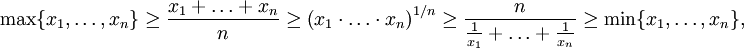
где каждое из равенств достигается только при
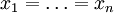 .
.См. также
Wikimedia Foundation. 2010.

![~A_d(x_1, \ldots, x_n) = \sqrt [d]{\sum_{i=1}^n x^d_i \over n}](/pictures/wiki/files/52/4377a1a1cca7febb67b6742c78083fe5.png)
![A_0(x_1, \ldots, x_n) = \lim_{d\to 0} A_d(x_1, \ldots, x_n) = \sqrt [n]{\prod_{i=1}^n x_i}](/pictures/wiki/files/99/ce639201193718a1aff85858ddaf4dcd.png)