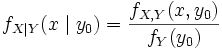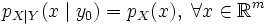Условная функция вероятности

Усло́вное распределе́ние в теории вероятностей — это распределение случайной величины при условии, что другая случайная величина принимает определённое значение.

Определения

Будем предполагать, что задано вероятностное пространство $(\Omega,\mathcal{F},\mathbb{P})$.

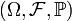Дискретные случайные величины

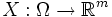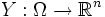Пусть $X: \Omega \to \mathbb{R}^m$ и $Y:\Omega \to \mathbb{R}^n$ — случайные величины, такие, что случайный вектор 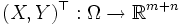$(X,Y)^{\top}:\Omega \to \mathbb{R}^{m+n}$ имеет дискретное распределение, задаваемое функцией вероятности 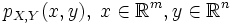$p_{X,Y}(x,y),\; x\in \mathbb{R}^m,y\in \mathbb{R}^n$. Пусть 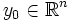$y_0 \in \mathbb{R}^n$ такой, что 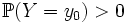$\mathbb{P}(Y = y_0) > 0$. Тогда функция

$p_{X \mid Y}(x \mid y_0) = \mathbb{P}(X = x \mid Y = y_0) = { p_{X,Y}(x,y_0) \over p_Y(y_0)}, \; x \in \mathbb{R}^m$,

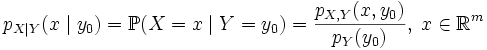где p_Y - функция вероятности случайной величины Y, называется усло́вной фу́нкцией вероя́тности случайной величины X при условии, что Y = y₀. Распределение, задаваемое условной функцией вероятности, называется условным распределением.

Абсолютно непрерывные случайные величины

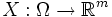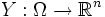Пусть $X: \Omega \to \mathbb{R}^m$ и $Y:\Omega \to \mathbb{R}^n$ - случайные величины, такие что случайный вектор 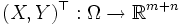$(X,Y)^{\top}:\Omega \to \mathbb{R}^{m+n}$ имеет абсолютно непрерывное распределение, задаваемое плотностью вероятности 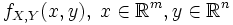$f_{X,Y}(x,y),\; x\in \mathbb{R}^m, y \in \mathbb{R}^n$. Пусть 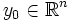$y_0 \in \mathbb{R}^n$ таково, что f_Y(y₀) > 0, где f_Y - плотность случайной величины Y. Тогда функция

$f_{X \mid Y}(x \mid y_0) = \frac{f_{X,Y}(x,y_0)}{f_Y(y_0)}$

называется усло́вной пло́тностью вероя́тности случайной величины X при условии, что Y = y₀. Распределение, задаваемое условной плотностью вероятности, называется условным распределением.

Свойства условных распределений

• Условные функции вероятности и условные плотности вероятности являются функциями вероятности и плотностями вероятности соответственно, то есть они удовлетворяют всем необходимым условиям. В частности,

• $p_{X\mid Y}(x\mid y_0) \ge 0,\; \forall x \in \mathbb{R}^m,\, y_0\in \mathbb{R}^n$,
• $\sum\limits_x p_{X \mid Y}(x \mid y_0) = 1,\; \forall y_0\in \mathbb{R}^n$,

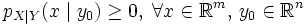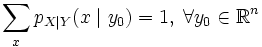и

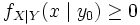• $f_{X\mid Y}(x\mid y_0) \ge 0$ почти всюду на $\mathbb{R}^{m+n}$,
• $\int\limits_{\mathbb{R}^m} f_{X \mid Y}(x \mid y_0)\, dx = 1,\; \forall y_0\in \mathbb{R}^n$,

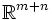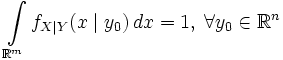• Справедливы формулы полной вероятности:

• $p_X(x) = \sum\limits_{y} p_{X\mid Y}(x \mid y)\, p_Y(y)$,
• $f_X(x) = \int\limits_{\mathbb{R}^n} f_{X \mid Y}(x\mid y)\, f_Y(y)\, dy$.

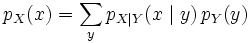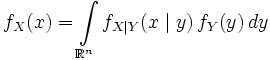• Если случайные величины X и Y независимы, то условное распределение равно безусловному:

$p_{X \mid Y}(x \mid y_0) = p_X(x),\; \forall x \in \mathbb{R}^m$

или

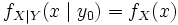$f_{X\mid Y}( x\mid y_0 ) = f_X(x)$ почти всюду на $\mathbb{R}^m$.

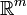Условные вероятности

Дискретные случайные величины

Если A - счётное подмножество 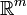$\mathbb{R}^m$, то

$\mathbb{P}(X \in A \mid Y = y_0) = \sum\limits_{x \in A} p_{X \mid Y}(x \mid y_0)$.

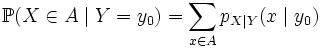Абсолютно непрерывные случайные величины

Если 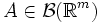$A \in \mathcal{B}(\mathbb{R}^m)$ - борелевское подмножество 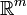$\mathbb{R}^m$, то полагаем по определению

$\mathbb{P}(X\in A \mid Y = y_0) = \int\limits_A f_{X \mid Y}(x \mid y_0)\, dx$.

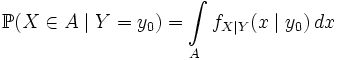Замечание. Условная вероятность в левой части равенства не может быть определена классическим способом, так как $\mathbb{P}(Y = y_0) = 0$.

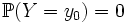Условные математические ожидания

Дискретные случайные величины

• Условное математическое ожидание случайной величины X при условии Y = y₀ получается суммированием относительно условного распределения:

$\mathbb{E}[X \mid Y = y_0 ] = \sum\limits_{x} x\, p_{X \mid Y}(x \mid y_0)$.

• Условное математическое ожидание X при условии случайной величины Y - это третья случайная величина $\mathbb{E}[X \mid Y]$, задаваемая равенством

$\mathbb{E}[X \mid Y](\omega) = \mathbb{E}[X \mid Y = Y(\omega)],\; \omega \in \Omega$.

Абсолютно непрерывные случайные величины

• Условное математическое ожидание случайной величины X при условии Y = y₀ получается интегрированием относительно условного распределения:

$\mathbb{E}[X \mid Y = y_0 ] = \int\limits_{\mathbb{R}^m} x\, f_{X \mid Y}(x \mid y_0)\, dx$.

• Условное математическое ожидание X при условии случайной величины Y - это третья случайная величина $\mathbb{E}[X \mid Y]$, задаваемая равенством

$\mathbb{E}[X \mid Y](\omega) = \mathbb{E}[X \mid Y = Y(\omega)],\; \omega \in \Omega$.