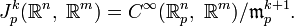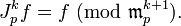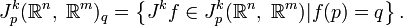Расслоение струй

Струя отображения f на многообразии M — это операция, сопоставляющая каждой точке x из M некоторый многочлен (урезанный многочлен Тейлора f в точке x). С точки зрения теории струй эти многочлены рассматриваются не как полиномиальные функции, а как абстрактные алгебраические многочлены, зависящие от точки многообразия.

Струи на евклидовом пространстве

Аналитическое определение

Струи и пространства струй могут быть определены, используя принципы математического анализа. Определение можно обобщить на гладкие отображения между банаховыми пространствами, аналитическими функциями в вещественной или комплексной области, на p-адический анализ и т. п.

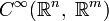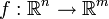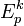Пусть $C^\infty(\mathbb{R}^n,\;\mathbb{R}^m)$ — векторное пространство гладких отображений $f:\mathbb{R}^n\rightarrow\mathbb{R}^m$. Пусть k — неотрицательное целое число, p — точка в $\mathbb{R}^n$. Определим класс эквивалентности $E_p^k$ в этом пространстве следующим образом: две функции f и g эквивалентны порядка k, если они имеют равное значение в точке p и все их частные производные до k-ого порядка включительно совпадают в этой точке.

Пространство k-струй (струй k-ого порядка) на 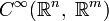$C^\infty(\mathbb{R}^n,\;\mathbb{R}^m)$ в точке p — это множество классов эквивалентности 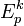$E^k_p$ (обозначается $J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)$).

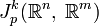k-струя гладкого отображения 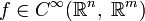$f\in C^\infty(\mathbb{R}^n,\;\mathbb{R}^m)$ в точке p — это класс эквивалентности в 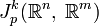$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)$, содержащий f.

Алгебро-геометрическое определение

Это определение основано на идеях алгебраической геометрии и коммутативной алгебры. Пусть 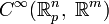$C^\infty(\mathbb{R}^n_p,\;\mathbb{R}^m)$ — векторное пространство ростков гладких отображений 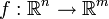$f:\mathbb{R}^n\rightarrow\mathbb{R}^m$ в точке 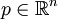$p\in\mathbb{R}^n$. 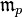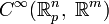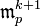Пусть $\mathfrak{m}_p$ — идеал отображений, равных нулю в точке p (это максимальный идеал локального кольца $C^\infty(\mathbb{R}^n_p,\;\mathbb{R}^m)$), а $\mathfrak{m}_p^{k+1}$ — идеал, состоящий из ростков всех отображений, равных нулю в точке p с точностью до k-ого порядка. Определим пространство струй в точке p как

$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)=C^\infty(\mathbb{R}^n_p,\;\mathbb{R}^m)/\mathfrak{m}_p^{k+1}.$

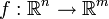Если $f:\mathbb{R}^n\rightarrow\mathbb{R}^m$ — гладкое отображение, то можно определить k-струю f в точке p как элемент 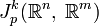$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)$, для которого

$J^k_pf=f\ (\hbox{mod}\ \mathfrak{m}_p^{k+1}).$

Теорема Тейлора

Независимо от определения, теорема Тейлора устанавливает канонический изоморфизм между векторными пространствами 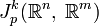$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)$ и $\mathbb{R}^m[z]/(z^{k+1})$, поэтому струи функций на евклидовом пространстве зачастую отождествляются с соответсвующими многочленами Тейлора.

Пространство струй из точки в точку

Мы определили пространство 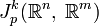$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)$ струй в точке 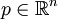$p\in\mathbb{R}^n$. Подпространство, содержащее те струи отображения f, для которых f(p) = q, обозначается

$J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)_q=\left\{J^kf\in J^k_p(\mathbb{R}^n,\;\mathbb{R}^m)|f(p)=q\right\}.$