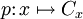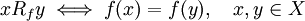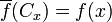- Класс эквивалентности
-
Отношение эквивалентности (
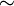 ) на множестве X — это бинарное отношение, для которого выполнены следующие условия:
) на множестве X — это бинарное отношение, для которого выполнены следующие условия:- Рефлексивность:
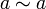 для любого a в X,
для любого a в X, - Симметричность: если
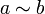 , то
, то 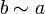 ,
, - Транзитивность: если
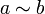 и
и 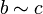 , то
, то 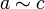 .
.
Запись вида «
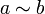 » читается как «a эквивалентно b».
» читается как «a эквивалентно b».Содержание
Связанные определения
- Классом эквивалентности C(a) элемента a называется подмножество элементов, эквивалентных a. Из вышеприведённого определения немедленно следует, что, если
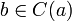 , то C(a) = C(b).
, то C(a) = C(b).
Множество всех классов эквивалентности обозначается
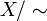 .
.- Множество классов эквивалентности по отношению
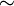 является разбиением множества.
является разбиением множества.
Примеры отношений эквивалентности
- Равенство («
 »), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел. - Сравнение по модулю, («а ≡ b (mod n)»).
- В Евклидовой геометрии
- Отношение конгруэнтности («
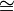 »).
»). - Отношение подобия («
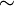 »).
»). - Отношение параллельности прямых («
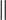 »).
»).
- Отношение конгруэнтности («
Факторизация отображений
Множество классов эквивалентности, отвечающее отношению эквивалентности
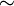 , обозначается символом X / ˜ и называется фактормножеством относительно
, обозначается символом X / ˜ и называется фактормножеством относительно 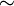 . При этом сюръективное отображение
. При этом сюръективное отображениеназывается естественным отображением (или канонической проекцией) X на фактормножество X / ˜.
Пусть X, Y — множества,
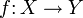 — отображение, тогда бинарное отношение
— отображение, тогда бинарное отношение 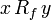 определённое правилом
определённое правиломявляется отношением эквивалентности на X. При этом отображение f индуцирует отображение
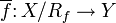 , определяемое правилом
, определяемое правиломили, что то же самое,
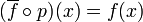 .
.
При этом получается факторизация отображения f на сюръективное отображение p и инъективное отображение
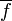 .
.Литература
- А. И. Кострикин Введение в алгебру. М.: Наука, 1977.
- Рефлексивность:
Wikimedia Foundation. 2010.