Предкомпакт

Компа́ктное простра́нство — это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие.

В топологии, компактные пространства по своим свойствам напоминают конечные множества в теории множеств.

Связанные определения

• Подмножество топологического пространства, являющееся в индуцированной топологии компактным пространством, называется компактным множеством.
• Множество называется относительно компактным или предкомпактным, если его замыкание компактно.
• Пространство называется секвенциально компактным, если из любой последовательности в нём можно выделить сходящуюся подпоследовательность.
• Локально компактное пространство — топологическое пространство, в котором любая точка имеет окрестность, замыкание которой компактно.
• Ограниченно компактное пространство — метрическое пространство, в котором все замкнутые шары компактны.
• Термин компакт иногда используется для метризуемого компактного пространства, но иногда просто как синоним к термину «компактное пространство».

Свойства

• Общие свойства:
  • Для любого непрерывного отображения образ компакта — компакт.
  • Замкнутое подмножество компакта компактно.
  • Компактное подмножество хаусдорфова пространства замкнуто.
  • Теорема Тихонова: произведение произвольного (необязательно конечного) множества компактных множеств (с топологией произведения) компактно .
  • Любое непрерывное взаимно однозначное отображение компакта в хаусдорфово пространство является гомеоморфизмом.
  • В компактных пространствах каждое центрированное семейство замкнутых множеств, т.е. семейство, в котором пересечения конечных подсемейств не пусты, имеет непустое пересечение. См. также Лемма о вложенных отрезках.

• Свойства компактных метрических пространств:
  • Метрическое пространство компактно тогда и только тогда, когда любая последовательность точек в нём содержит сходящуюся подпоследовательность.
  • Для конечномерных евклидовых пространств подпространство является компактом тогда и только тогда, когда оно ограничено и замкнуто. Про пространства, обладающие таким свойством, говорят, что они удовлетворяют свойству Гейне — Бореля. См. также Теорема Больцано — Вейерштрасса.
  • Лемма Лебега: Для любого компактного метрического пространства и открытого покрытия 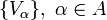$\{V_\alpha\},\ \alpha\in A$ существует положительное число $\,\! r$ такое, что любое подмножество, диаметр которого меньше $\,\! r$, содержится в одном из множеств $\,\! V_\alpha$. Такое число $\,\! r$ называется числом Лебега.
  • В компактных пространствах каждый ультрафильтр сходится по крайней мере к одной точке.

Примеры компактных множеств

• замкнутые и ограниченные множества в $\mathbb{R}^n$
• конечные подмножества в пространствах, удовлетворяющих аксиоме отделимости $\mathbf{T}_1$
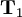
• теорема Асколи — Арцела даёт характеризацию компактных множеств для некоторых функциональных пространств. Рассмотрим пространство C(X) вещественных функций на метрическом компактном пространстве X с нормой 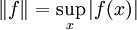$\|f\|=\sup_x |f(x)|$. Тогда замыкание множества функций F в C(X) компактно тогда и только тогда, когда F равномерно ограничено и равностепенно непрерывно.
• пространство Стоуна булевых алгебр
• компактификация топологического пространства

История

Бикомпактное пространство — термин, введённый П. С. Александровым как усиление введённого М. Фреше понятия компактного пространства: топологическое пространство компактно — в первоначальном смысле слова — если в каждом счётном открытом покрытии этого пространства содержится его конечное подпокрытие. Однако дальнейшее развитие математики показало, что понятие бикомпактности настолько важнее первоначального понятия компактности, что в настоящее время под компактностью понимают именно бикомпактность, а компактные в старом смысле пространства называют счётно-компактными. Оба понятия равносильны в применении к метрическим пространствам.

Литература

• О. Я. Виро, О. А. Иванов, В. М. Харламов и Н. Ю. Нецветаев. Задачный учебник по топологии
• Л.Шварц, Анализ, т. I, М., МИР, 1972.