- Хаусдорфово пространство
-
Хаусдорфово пространство — топологическое пространство, удовлетворяющее сильной аксиоме отделимости. Названо в честь Ф. Хаусдорфа, одного из основоположников общей топологии. Его первоначальное определение топологического пространства включало в себя требование, которое теперь называется хаусдорфовостью. Иногда для обозначения структуры хаусдорфового топологического пространства на множестве применяется термин хаусдорфова топология.
Определение
Топологическое пространство
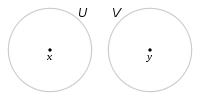
 называется хаусдорфовым, если любые две различных точки
называется хаусдорфовым, если любые две различных точки  ,
,  из
из  обладают непересекающимися окрестностями
обладают непересекающимися окрестностями  ,
,  .
.Примеры и контрпримеры
- Хаусдорфовы
- Хаусдорфовыми являются все метрические пространства и метризуемые пространства, в частности:
- евклидовы пространства

- многообразия
- большинство используемых в анализе бесконечномерных функциональных пространств, таких как
 или
или  ,
,  .
.
- евклидовы пространства
- По определению, топологические группы являются хаусдорфовыми.
- Хаусдорфовыми являются все метрические пространства и метризуемые пространства, в частности:
- Нехаусдорфовы
- Не является хаусдорфовой, например, топология Зарисского на алгебраическом многообразии.
- Нехаусдорфов, вообще говоря, спектр кольца.
- Простейший (и важный) пример нехаусдорфова пространства — связное двоеточие, а в более общем случае — алгебры Гейтинга.
Свойства
- Единственность предела последовательности (в более общем случае — фильтра), если таковой предел существует.
- Свойство, равносильное определению хаусдорфовости топологии, — замкнутость диагонали
 в декартовом квадрате
в декартовом квадрате  пространства
пространства  .
. - В хаусдорфовом пространстве замкнуты все его точки (то есть одноточечные множества).
- Подпространство и декартово произведение хаусдорфовых пространств тоже хаусдорфовы.
- Вообще говоря, хаусдорфовость не передаётся факторпространствам.
- Компактное хаусдорфово пространство нормально и оно метризуемо тогда и только тогда, когда имеет счетную базу топологии.
В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 15 мая 2011.Категория:- Общая топология
- Хаусдорфовы
Wikimedia Foundation. 2010.