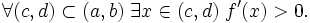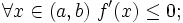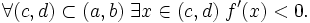- Невозрастающая функция
-
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной.
Содержание
Определения
Пусть дана функция
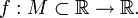 Тогда
Тогда- функция f называется возраста́ющей на M, если
-
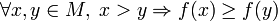 .
.
- функция f называется стро́го возраста́ющей на M, если
-
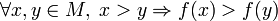 .
.
- функция f называется убыва́ющей на M, если
-
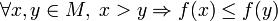 .
.
- функция f называется стро́го убыва́ющей на M, если
-
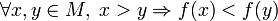 .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Другая терминология
Иногда возрастающие функции называют неубыва́ющими, а убывающие функции невозраста́ющими. Строго возрастающие функции тогда зовут просто возрастающими, а строго убывающие просто убывающими.
Свойства монотонных функций
- Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
- Монотонная функция,
![f:[a,b] \to \R,](/pictures/wiki/files/52/41d5e5df5fda23d3bc1807b596641aa0.png) определённая на замкнутом интервале, ограничена. В частности, она интегрируема по Лебегу.
определённая на замкнутом интервале, ограничена. В частности, она интегрируема по Лебегу. - Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
- Монотонная функция
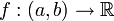 дифференцируема почти всюду относительно меры Лебега.
дифференцируема почти всюду относительно меры Лебега.
Условия монотонности функции
- (Критерий монотонности функции, имеющей производную на интервале) Пусть функция
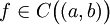 непрерывна на (a,b), и имеет в каждой точке
непрерывна на (a,b), и имеет в каждой точке 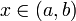 производную f'(x). Тогда
производную f'(x). Тогда
- f возрастает на (a,b) тогда и только тогда, когда
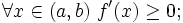
- f убывает на (a,b) тогда и только тогда, когда
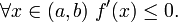
- f возрастает на (a,b) тогда и только тогда, когда
- (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция
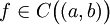 непрерывна на (a,b), и имеет в каждой точке
непрерывна на (a,b), и имеет в каждой точке 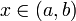 производную f'(x). Тогда
производную f'(x). Тогда
- если
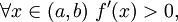 то f строго возрастает на (a,b);
то f строго возрастает на (a,b); - если
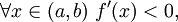 то f строго убывает на (a,b).
то f строго убывает на (a,b).
- если
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место
- (Критерий строгой монотонности функции, имеющей производную на интервале) Пусть
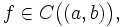 и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
Примеры
- Экспонента f(x) = ex строго возрастает на всей числовой прямой.
- Парабола f(x) = x2 строго убывает на
![(-\infty,0]](/pictures/wiki/files/102/f9d75a40b8eadac31117745d2255ef61.png) и строго возрастает на
и строго возрастает на 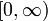 .
. - Константа
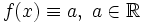 одновременно возрастает и убывает на всей числовой прямой.
одновременно возрастает и убывает на всей числовой прямой. - Канторова лестница — пример непрерывной монотонной функции, которая не является константой, но при этом имеет производную равную нулю в почти всех точках.
- Функция Минковского — пример сингулярной строго возрастающей функции.
См. также
Wikimedia Foundation. 2010.