МЕТРИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ

- раздел теории чисел, в к-ром изучаются и метрически (т. е. на основе теории меры )характеризуются множества чисел, обладающих определенными арифметич. свойствами. М. т. ч. тесно связана с теорией вероятностей, что иногда дает возможность использовать ее методы и результаты для анализа теоретико-числовых моделей.

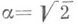Многие задачи, касающиеся арифметич. свойств отдельных чисел, допускают также метрич. постановку; напр., наряду с вопросом о том, будет ли равномерно распределена последовательность дробных долей , при или 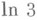, можно ставить вопрос о том, какова мера Лебега тех 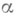из интервала (0,1), для к-рых эта последовательность равномерно распределена. Такое метрич. обобщение задачи часто оказывается весьма полезным и дает возможность представить явление в целом. Иногда на основе метрич. рассуждений без особого труда удается доказать существование чисел с определенными арифметич. свойствами, тогда как прямое построение таких чисел бывает сложным (нормальные числа Бореля, числа с определенными свойствами аппроксимации и т. п.).

Наиболее значительные достижения М. т. ч. относятся к диофантовых приближений метрической теории, к теории равномерного распределения числовых последовательностей, к теории цепных дробей и др. областям теории чисел.

Одной из первых теорем М. т. ч. является теорема Бореля (Е. Borel, 1909): почти все (в смысле меры Лебега) действительные числа а. интервала (0, 1) нормальны в системе счисления с любым целым основанием g. В другой равносильной формулировке эта теорема утверждает, что дробные доли равномерно распределены на интервале (0, 1). Теорема Бореля обобщалась и углублялась многими математиками. Плодотворной оказалась точка зрения, основанная на том, что "цифры" 0, 1, . . ., g-1, встречающиеся в разложении aв системе счисления с основанием g(g-ичной системе), являются независимыми случайными величинами. Явно или неявно основываясь на этом обстоятельстве и применяя методы, разработанные в теории вероятностей для отыскания асимптотич. законов распределения сумм независимых и слабо зависимых случайных величин, были решены основные вопросы, касающиеся распределения "цифр" 0,1, . . ., g-1, и произвольных групп "цифр" в g-ичном разложении чисел , "случайно" выбираемых в интервале (0,1). Напр., полагая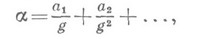

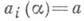где а _i- числа ряда 0, 1, . . ., g-1, находят, что а _i = а _i(a) можно рассматривать как независимые случайные величины, определенные на интервале (0, 1) с мерой Лебега на этом интервале в качестве вероятностной меры. Если а- любое число ряда 0,1, . . ., g-1, k_n(a).- число тех , для к-рых при данном а, то

распределяется асимптотически по нормальному закону, т. е. при любом действительном хмера множества тех а, для к-рых

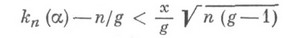
при 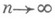стремится к пределу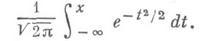

Г. Вейль (Н. Weyl, 1916) доказал, что если а _n , n= 1, 2, . . ., - произвольная возрастающая последовательность натуральных чисел, то для почти всех a дробные доли {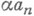} равномерно распределены на интервале (0, 1). В предположении, что а _п являются значениями нек-рой функции, определенной на бесконечном интервале (1,) и обладающей специальными аналитич. словиями, эта теорема допускает уточнения, касающиеся "качества" равномерного распределения. И. Коксма [8] доказал общую теорему о распределении дробных долей функции двух переменных f(a, п), где a - действительное переменное, принимающее почти все значения из интервала (1, 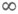), а n=1, 2, ... . Напр., дробные доли {a ⁿ}для почти всех a>1 равномерно распределены на интервале (0, 1).

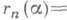
Помимо вопросов, связанных с нормальными числами Бореля, одним из основных объектов М. т. ч. в начале ее развития была метрич. теория цепных дробей. Пусть a.- действительное число из интервала (0, 1), a=[0, a₁, . . .] - его разложение в цепную дробь, - знаменатель п-йподходящей дроби [0, а ₁ , . . ., а _п]. А. <Я. Хинчин установил (1935), что для почти всех 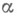при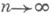

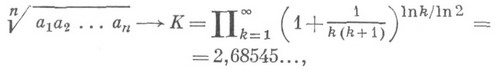
и существует такая абсолютная постоянная 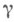, что для почти всех a. будет 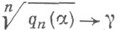при 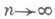. П. Леви (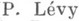) нашел, что 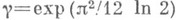. Кроме того, А. Я. Хинчин [5] использовал полученные им результаты о метрич. свойствах цепных дробей для доказательства теоремы о приближении чисел рациональными. Пусть f(x)- положительная непрерывная функция положительного аргумента х, причем 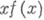- невозрастающая функция. Тогда неравенство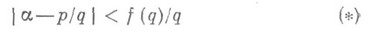

имеет для почти всех а бесконечное множество решений в целых ри q(g>0), если при нек-ром с>0 интеграл

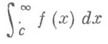
расходится; напротив, неравенство (*) имеет для почти всех a не более конечного числа решений в целых ри q(q>0), если интеграл сходится для всех с>0. Эта теорема переосмысливалась и обобщалась с различных точек зрения. Она стала исходным пунктом интенсивного развития метрич. теории диофантовых приближений. П. Эрдёш [7], завершая серию работ своих предшественников, получил следующие результаты. Необходимое и достаточное условие того, что для почти всех a. бесконечное число 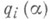содержится в произвольной последовательности 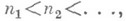есть

где 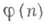- функция Эйлера. При этом же условии для почти всех a. неравенство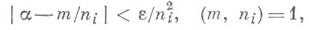

где т- целое, e>0 - любое, имеет бесконечное число решений: Эти результаты близки к гипотезе (1982): если n₁<n₂ < . . . - произвольная последовательность целых чисел, d_i > 0 - любые, то неравенство

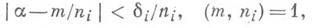
имеет бесконечное число решений для почти всех a. тогда и только тогда, когда

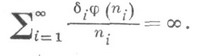
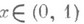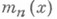Р. О. Кузьмин доказал (1928), что при любом мера множества тех a, для к-рых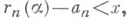

равна

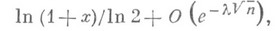
где 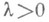- абсолютная постоянная. Асимптотич. соотношение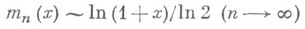

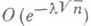было известно К. Гауссу (С. Gauss), но он не опубликовал его, а в одном из писем к П. Лапласу (P. Laplace) указывал, что было бы весьма желательно оценить разность Оценка Кузьмина была улучшена П. Леви (1929) до 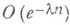Метод Кузьмина явился источником многих других метрич. теорем о цепных дробях.

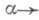
Современная трактовка метрич. вопросов, связанных с нормальными числами Бореля и с теорией цепных дробей, использует идеи эргодич. теории. Это основано на том, что отображения интервала (0, 1) на себя 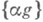и 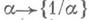, тесно связанные с разложением a в g-ичную дробь и цепную дробь соответственно, являются сохраняющими меру и эргодическими: первое сохраняет меру Лебега, второе- меру m(A), определяемую для каждого измеримого множества Аиз (0,1) формулой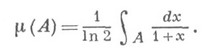

С этой точки зрения теорема Гаусса - Кузьмина без оценки остаточного члена непосредственно следует из индивидуальной эргодич. теоремы Биркгофа. Соображения эргодич. теории оказываются полезными и при оценке остатков в нек-рых предельных теоремах. Напр., результаты А. Я. Хинчина допускают (см. [10]) уточнение:

где 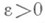- произвольно. Идеи эргодич. теории оказываются полезными и во многих других задачах М. т. ч. (линейные диофантовы приближения, распределение значений матричной показательной функции, алгоритм Якоби - Перрона и др.).

В нек-рых случаях метрич. характеристика числовых множеств, основанная на мере Лебега, оказывается слишком грубой, и тогда применяют более тонкие характеристики, напр, размерности Хаусдорфа. Такой подход оказывается особенно полезным в теории дио-фантовых приближений и теории трансцендентных чисел. Напр., было установлено [6], что при любых фиксированных 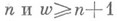множество тех действительных чисел х, для к-рых неравенство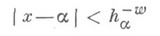

имеет бесконечное число решений в алгебраич. числах а степени п и высоты 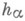, имеет размерность Хаусдорфа, равную 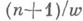. Если то 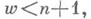соответствующее неравенство имеет бесконечное число решений для почти всех х, в то время как предполагается, что это верно для всех х (гипотеза Вирзинга). Аналогичные результаты известны для комплексных чисел. Они непосредственно связаны с фундаментальными вопросами классификации трансцендентных чисел [3].

С метрич. точки зрения анализируются не только задачи, касающиеся действительных и комплексных чисел, но также р-адических чисел, аделей, формальных степенных рядов и т. д. и вообще элементов всех пространств, в к-рых введена мера и в к-рых ставится "арифметическая" задача. В частности, для р-адических чисел верны аналоги многих метрич. теорем теории равномерного распределения и теории диофантовых приближений действительных чисел, несмотря на то, что область р-адических чисел отличается своей метрикой и топологией (см. [3], [9]).

Метрич. подход оказывается эффективным при решении "некорректно" поставленных задач, когда недостаток информации об объекте исследования компенсируется допущением "случайного" выбора этого объекта из нек-рого множества сходных объектов. При этом, конечно, не удается исследовать первоначальный объект, что иногда в принципе невозможно из-за недостатка информации о нем, но получаются выводы, что "почти все" объекты из рассматриваемого множества обладают определенными свойствами. Напр., пусть 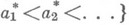- последовательность натуральных чисел, возрастающая не быстрее нек-рой степени, т. е. 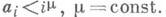Ставится вопрос, существует ли такое число r, что любое натуральное число можно представить суммой не более чем rслагаемых из 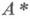. Ясно, что имеющейся информации о последовательности 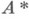недостаточно для решения задачи.

Пусть 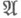- множество последовательностей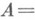 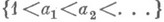целых чисел, где каждое 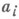"случайно" выбирается из отрезк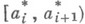а . На 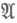можно определить меру Лебега и доказать, что для почти всех Асуществует искомое число 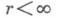(см. [4]).

Весьма содержательной и глубокой является связь между "глобальными" утверждениями М. т. ч. и их "индивидуальными" реализациями. Несмотря на то, что почти все элементы нек-рого множества обладают определенным свойством, бывает очень трудно установить, что данный конкретный элемент этого множества обладает этим же свойством. Напр., Э. Борель высказал предположение, что такие числа, как и т. д., нормальны, и хотя почти все числа нормальны, до сих пор (1982) неизвестно, является ли нормальным хотя бы одно из этих чисел. Во многих случаях доказать метрич. теорему легче, чем подобную "индивидуальную". Однако это не означает, что в М. т. ч. нет глубоких проблем, т. к. многие проблемы М. т. ч. тесно связаны с нек-рыми "индивидуальными" проблемами, что иногда обнаруживается достаточно быстро. С другой стороны, решение "индивидуальных" проблем обнаруживает их связь с метрическими.

Идеи М. т. ч. играют фундаментальную роль во многих разделах аналитич. теории чисел, в особенности тогда, когда используется интегрирование по нек-рой мере. В этих случаях вывод какой-либо метрич. теоремы не является целью исследования, но метрич. со-ебражения используются как промежуточный этап рассуждений. Они могут быть одним из главных принципов, лежащих в основе рассуждения, хотя окончательная формулировка результата не будет содержать никаких метрич. понятий. Примером систематич. использования такого рода рассуждений является метод Харди - Литлвуда - Виноградова, в к-ром существенную роль играют метрич. свойства приближения чисел рациональными дробями ("большие" и "малые" дуги Харди - Литлвуда). Это обстоятельство позволило И. М. Виноградову формулировать свои новые теоремы об оценках сумм Вейля как нек-рые метрич. теоремы [1]. Кроме того, метод И. М. Виноградова оценок сумм Вейля носит ярко выраженный метрич. характер, где устанавливается связь между "глобальной" оценкой интеграла и "индивидуальной" оценкой конкретной суммы. Примеров такого рода в теории чисел мало.

Лит.:[1] Виноградов И. <М., Метод тригонометрических сумм в теории чисел, М., 1971: [2] Постников А. Г., "Тр. Матем. ин-та АН СССР", 1966, т. 82, с. 3-111; [3] Спринджук В. Г., Проблема Малера в метрической теории чисел, Минск, 1967; [4] его же, "Известия АН БССР. Сер. Физ.-матем. наук", 1970, № 1, с. 5-14; [5] Xинчин А. Я., Цепные дроби, 4 изд., М., 1978; [6] Вакеr A., Schmidt W., "Рrос. London Math. Soc", (3), 1970, v. 21, p. 1-11; [7] Erdos P., "J. Number Theory", 1970, v. 2, p. 425-41; [8] Кокsma J. F., Diophantische Approximationen, В., 1936; [9] Lutz E., Sur les approximations diophantiennes lineaires p-adiques, P., 1955; [10] Philipp W., "Pacific J. Math.", 1967, v. 20, № 1, 109- 27; Циглер И., Хельмберг Г., "Математика", 1963, т. 7, № 3, с. 3-46.

В. Г. Спринджук.